随机变量及其分布函数的概念、性质及应用

随机变量的概念

分布函数的概念及性质

• 概念
  
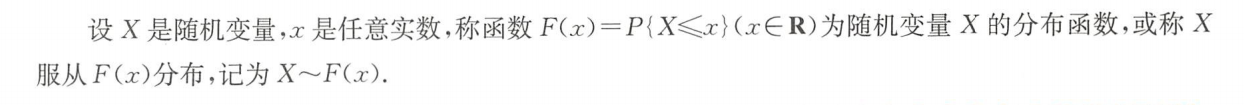
• 性质(也是充要条件)
  
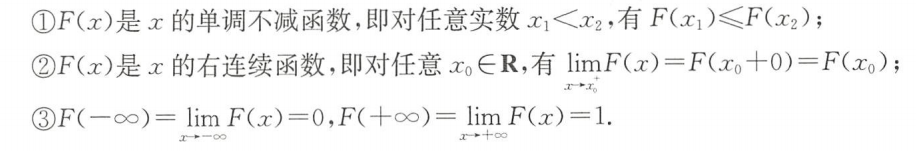
• 注意：
  • 务必记住分布函数是时间的概率，由此知 0 ≤ F(x) ≤ 1,即F(x)是有界函数
  • 满足以上三条性质的函数F(x)必是某个随机变量X的分布函数，所以，这三条性质也是判断函数F(x)是否为某一随机变量X的分布函数的充要条件。

分布函数的应用—求概率

• P{X ≤ a} = F(a)
• P{X < a} = F(a - 0)
• p{x = a} = F(a) - F(a - 0) —> F(a - 0) 是表示a的左极限，及从左边趋近于a的值