B树的插入和删除
B树的插入和删除
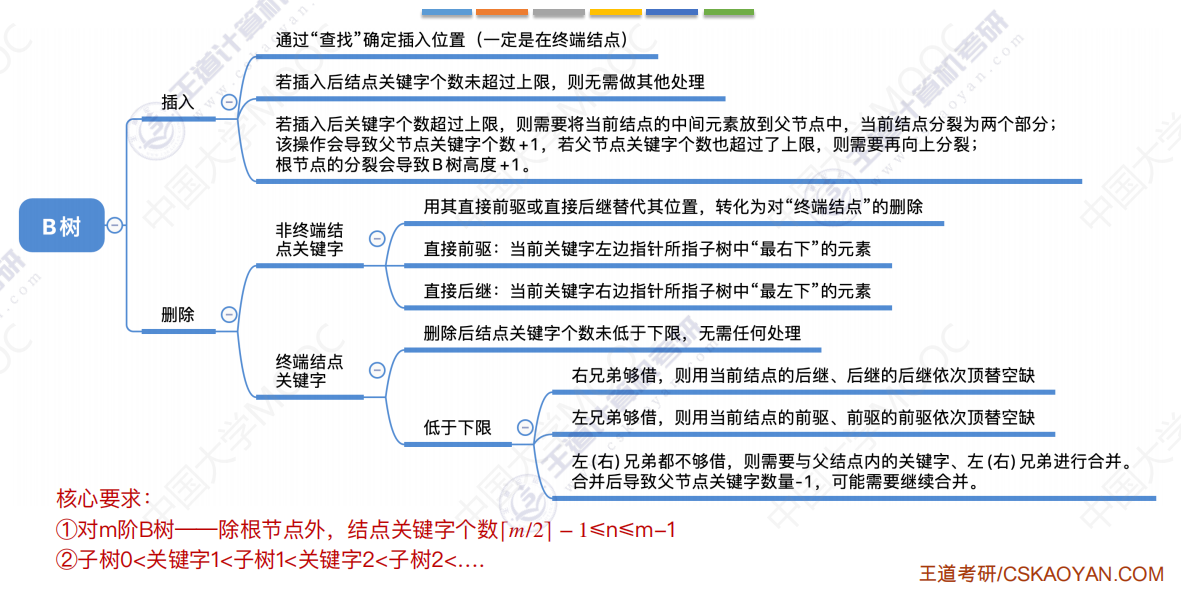
B树的插入
- 在B树中搜索插入位置:
- 从根节点开始,根据插入的关键字,向下逐层搜索合适的插入位置。
- 如果关键字已经存在于B树中,根据需要更新节点的值或执行其他操作。
- 在叶子节点中插入关键字:
- 如果找到了合适的叶子节点,将关键字插入到该节点中的适当位置。插入过程可以采用二分查找的方式,保持关键字的有序性。
- 检查叶子节点是否上溢:
- 如果插入关键字后,叶子节点的关键字个数超过了B树的阶数,则发生了上溢。
- 解决上溢的方法是将该叶子节点进行分裂。
- 叶子节点的分裂:
- 将关键字分成两部分,将较小的一部分保留在原叶子节点中,将较大的一部分放入一个新的叶子节点中。
- 选择一个中间位置的关键字,作为新的节点的分割点。
- 将新的叶子节点插入到原叶子节点的右侧。
- 更新父节点:
- 将新的叶子节点的分割点关键字插入到原叶子节点的父节点中,同时调整父节点的子节点指针。
- 如果父节点上溢,则继续递归执行分裂和更新父节点的操作。
- 逐级向上更新父节点:
- 如果插入关键字导致父节点上溢,则执行类似的分裂和更新父节点的操作,直到根节点。
- 如果根节点上溢,则执行根节点的分裂。
- 根节点的分裂:
- 如果根节点发生分裂,创建一个新的根节点,并将原根节点分裂后的两个节点作为子节点插入到新根节点中。
- 插入完成:
- 插入操作完成后,B树的结构保持平衡,即满足B树的定义和性质。

- 插入操作完成后,B树的结构保持平衡,即满足B树的定义和性质。
B树的删除
- 定位到要删除的关键字所在的叶子节点。
- 从根节点开始,通过比较关键字大小,沿着树向下遍历,直到达到叶子节点。
- 删除关键字。
- 如果要删除的关键字存在于叶子节点上,直接删除它。
- 如果要删除的关键字不在叶子节点上,需要进行下面的调整。
- 处理删除后的节点。
- 如果删除关键字后,关键字数量仍大于等于B树的最小度数(通常为节点关键字数的一半),则删除操作完成,不需要进一步调整。
- 如果删除后的节点关键字数量小于最小度数,需要进行下列调整操作:
- 借用相邻节点的关键字:
- 如果相邻节点的关键字数量大于最小度数,可以从相邻节点借用一个关键字到当前节点,同时将一个父节点的关键字下移至当前节点。
- 如果相邻节点的关键字数量不足以借用,进入下一步的合并操作。
- 合并节点:
- 如果无法借用关键字,则需要将当前节点与一个相邻节点合并。
- 合并操作将两个节点合并成一个新的节点,包括合并它们的关键字和子节点。
- 合并操作可能涉及到父节点的更新,以确保B树的平衡性。
- 递归调整:
- 如果删除和合并操作影响到了父节点,需要递归地进行调整,以保持整棵B树的平衡性。
总结