二叉排序树(BST)
二叉排序树
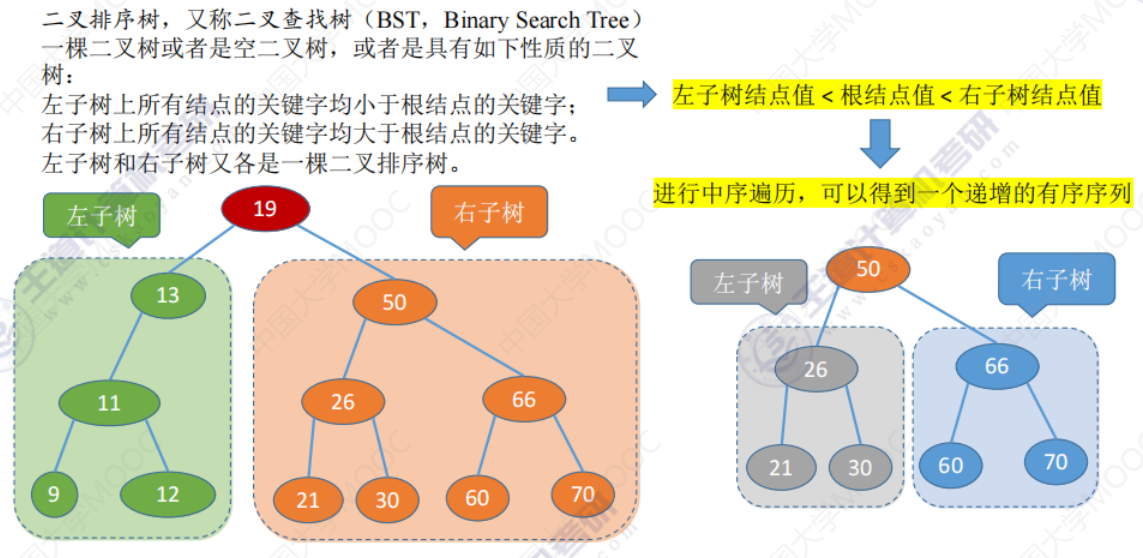
二叉排序树的定义
- 若左子树非空,则左子树上所有结点的值均小于根结点的值。
- 若右子树非空,则右子树上所有结点的值均大于根结点的值
- 左、右子树也分别是一颗二叉排序树。
二叉排序树的查找
二叉排序树中查找某关键字时,查找过程类似于次优二叉树,在二叉排序树不为空树的前提下,首先将被查找值同树的根结点进行比较,会有 3 种不同的结果:
- 如果相等,查找成功;
- 如果比较结果为根结点的关键字值较大,则说明该关键字可能存在其左子树中;
- 如果比较结果为根结点的关键字值较小,则说明该关键字可能存在其右子树中;
- 实现函数为:(运用递归的方法)
1
2
3
4
5
6
7BSTNode *BST_Search(BSTree T,int key){
while(T != NULL && key != T->key){ // 若树空或等于根结点值,则结束循环
if(key < T->key) T = T->lchild; // 小于,则在左子树上查找
else T = T->rchild; // 大于,则在右子树上查找
}
return T;
}
二叉排序树中插入关键字
- 二叉排序树作为一种动态树表,其特点是树的结构通常不是一次生成的,而是在查找过程中,当树中不存在关键字值等于给定值的结点时再进行插入的。
- 插入结点的过程如下:若原二叉排序树为空,则直接插入;否则,若关键字k小于根结点值,则插入到左子树,若关键字k大于根结点值,则插入到右子树。插入的结点一定是一个新添加的叶结点,且是查找失败时的查找路径上访问的最后一个结点的左孩子或右孩子。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15// 在二叉排序树中插入关键字为 k 的新结点(递归实现)
int BST_Insert(BSTree *T,int k){
if((*T) == NULL){ // 原树为空,新插入的结点为根节点
(*T )= (BSTree) malloc(sizeof (BSTNode));
(*T)->key = k;
(*T)->lchild = (*T)->rchild = NULL;
return 1; //返回1,插入成功
}
else if(k == (*T)->key) //树中存在相同关键字的结点,插入失败
return 0;
else if(k < (*T)->key) // 插入到T的左子树
return BST_Insert(&((*T)->lchild),k);
else // 插入到T的右子树
return BST_Insert(&((*T)->rchild),k);
}
二叉排序树的构造
1 | |
二叉树排序树的删除
- 若被删除的结点z是叶结点,则直接删除,不会破坏二叉排序树的性质。
- 若结点只有一颗左子树或右子树,则让z的子树称为z的父结点的子树,替代z的位置。
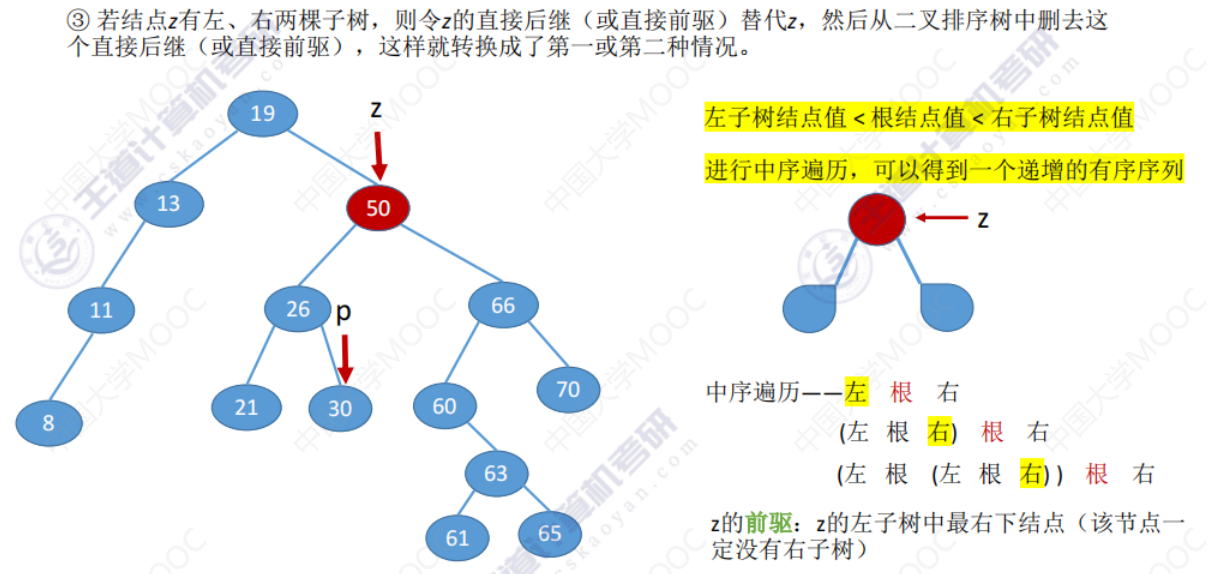
- 若结点z有左、右子树,有两种方法
- 令z的直接后继代替z,然后从二叉排序树中删去这个直接后继。z的直接后继–>z的右子树中最左下结点(该结点一定没有左子树)
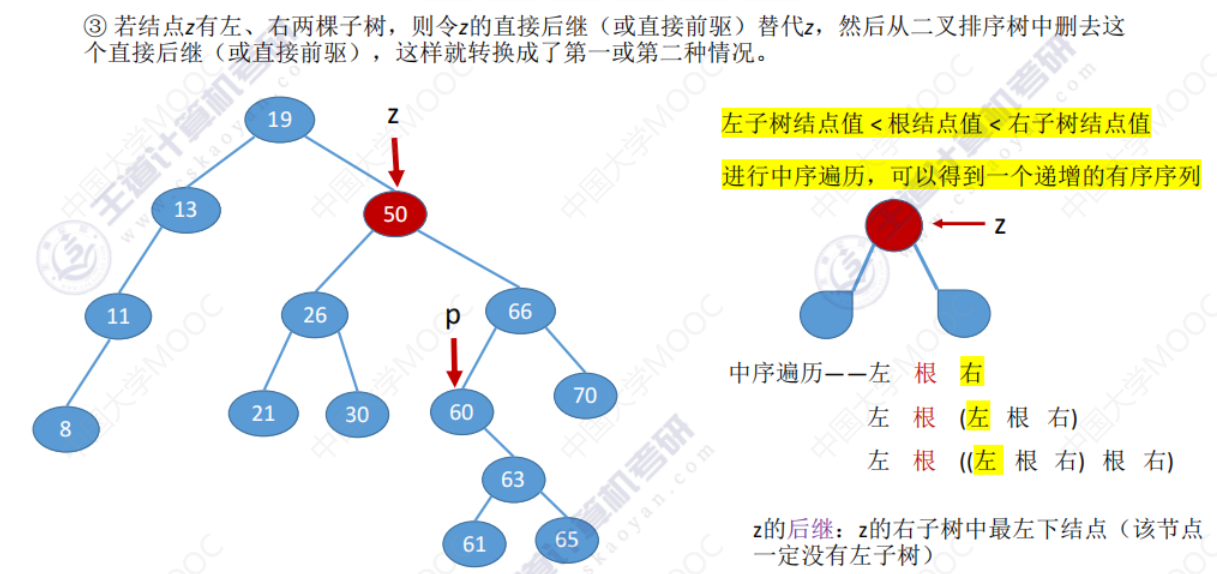
- 令z的直接前驱代替z,然后从二叉排序树中删去这个直接前驱。z的直接前驱–>z的左子树中最右下结点(该结点一定没有右子树)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35// 二叉排序树的删除
BSTree Delete_BST(BSTree *T,int data) {
if ((*T) == NULL) {
printf("要删除的元素不存在!\n");
return NULL;
} else if ((*T)->key == data) {
if ((*T)->lchild == NULL && (*T)->rchild == NULL) {
free(*T);
*T = NULL;
} else if ((*T)->lchild == NULL) {
BSTree temp = *T;
(*T) = (*T)->rchild;
free(temp);
} else if ((*T)->rchild == NULL) {
BSTree temp = (*T);
(*T) = (*T)->lchild;
free(temp);
} else {
BSTree pre = (*T)->lchild;
while (pre->rchild != NULL) {
pre = pre->rchild;
}
(*T)->key = pre->key;
(*T)->lchild = Delete_BST(&((*T)->lchild),pre->key);
}
}
else if((*T)->key < data){
(*T)->rchild = Delete_BST(&((*T)->rchild),data);
}else{
(*T)->lchild = Delete_BST(&((*T)->lchild),data);
}
return (*T);
}
- 令z的直接后继代替z,然后从二叉排序树中删去这个直接后继。z的直接后继–>z的右子树中最左下结点(该结点一定没有左子树)
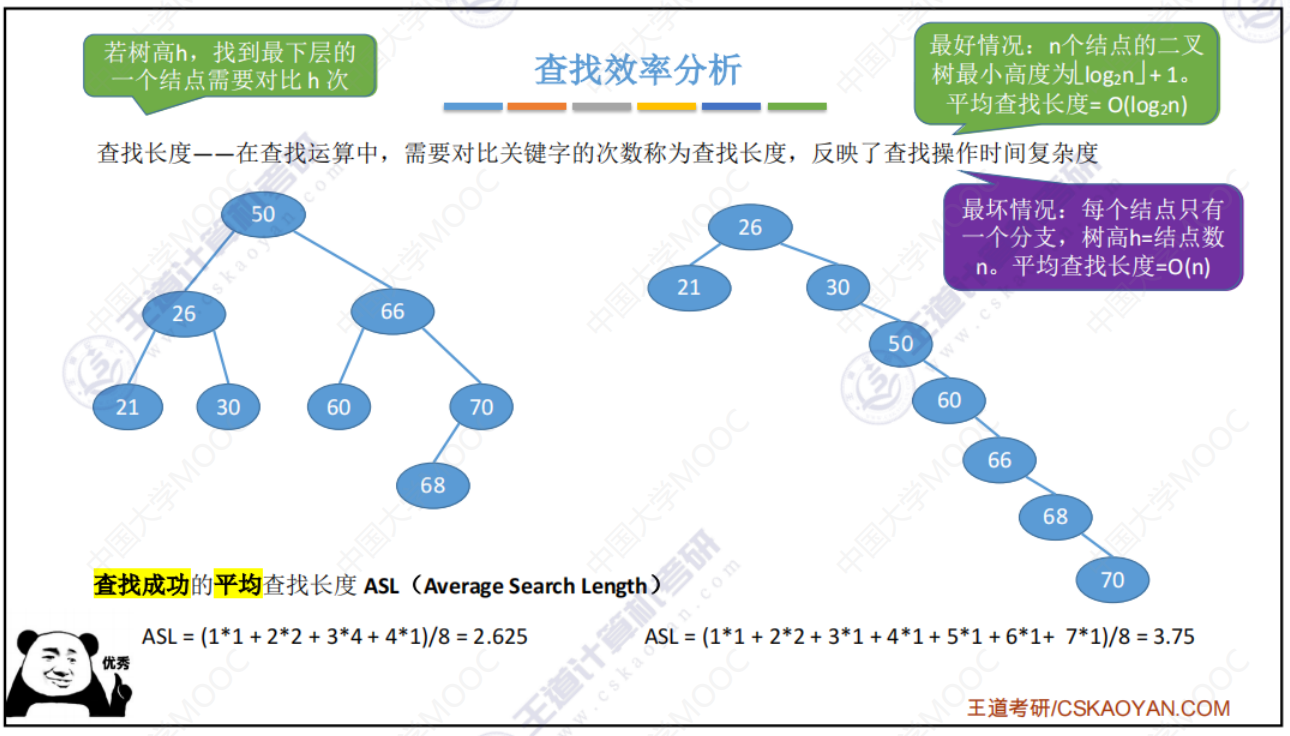
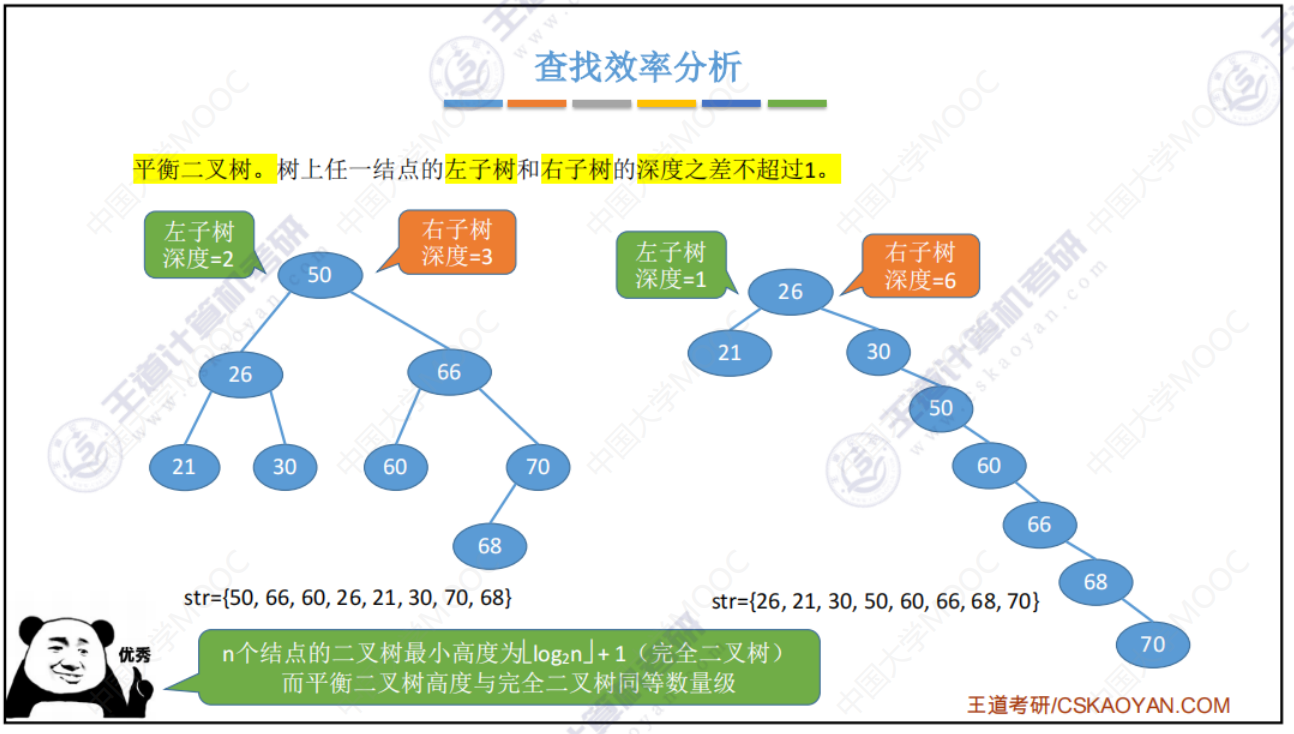
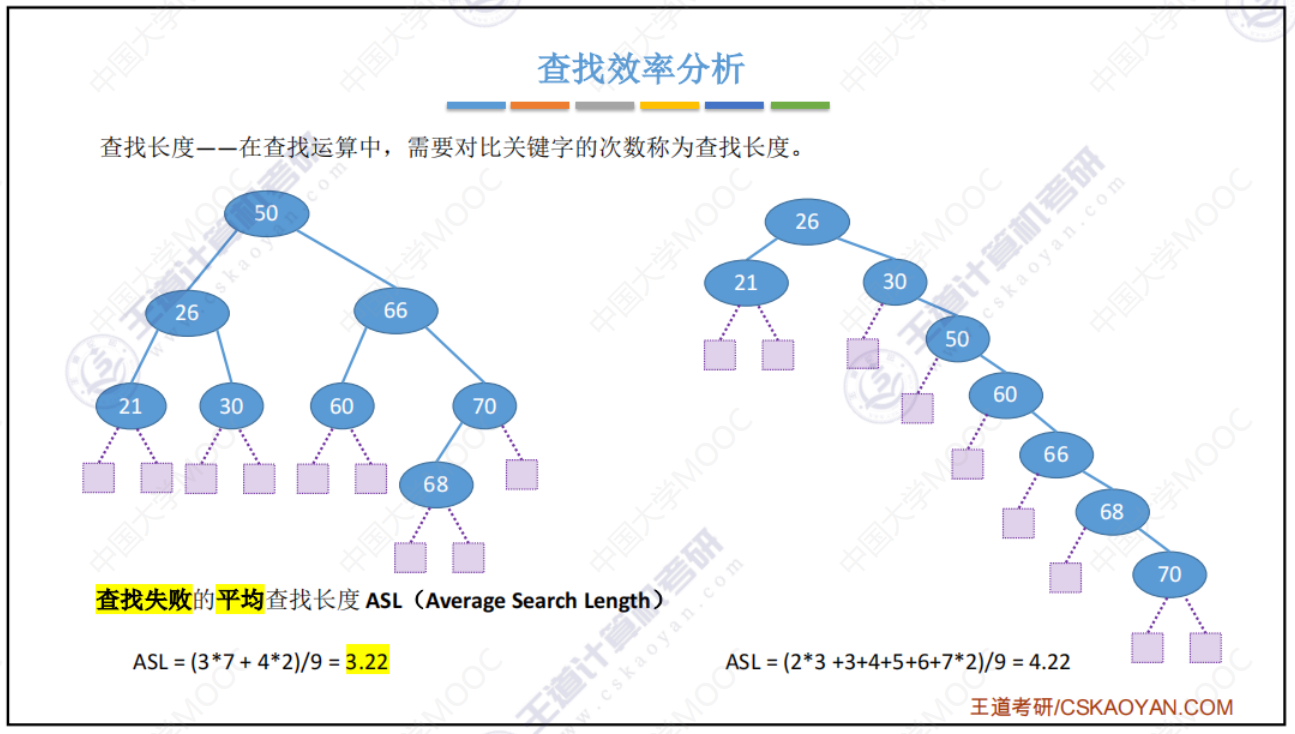
查找效率分析
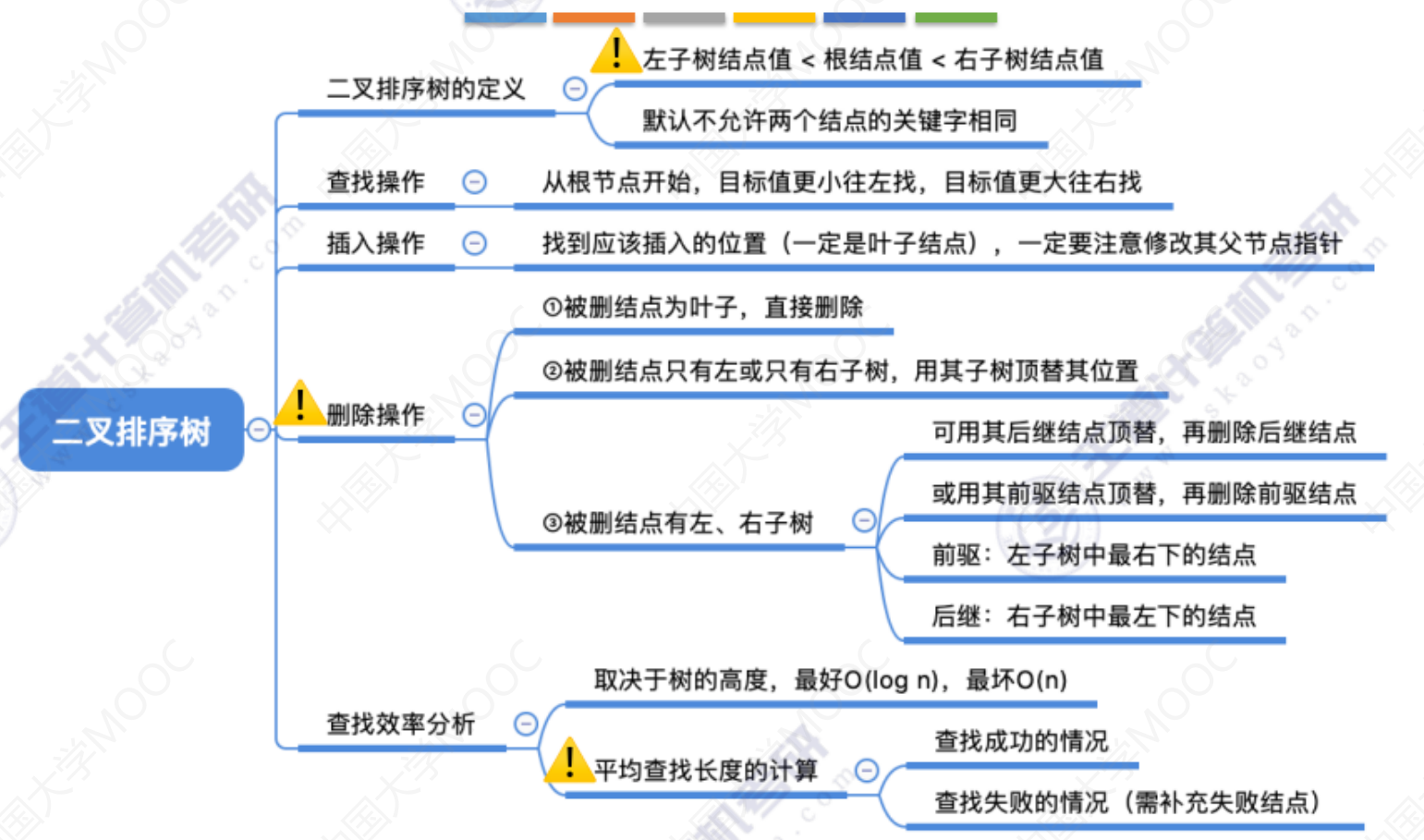
总结
完整代码
1 | |