折半查找

• 折半查找，又称“二分查找”，仅适用于有序的顺序表。—>因为顺序表拥有随机访问的特性，链表没有。

算法的思想

• 折半查找的基本思想：首先将给定值key与表中中间位置的元素（mid的指向元素）比较。mid=low+high/2（向下取整）
• 若key与中间元素相等，则查找成功，返回该元素的存储位置，即mid；
• 若key与中间元素不相等，则所需查找的元素只能在中间元素以外的前半部分或后半部分。（至于是前半部分还是后半部分要看key与mid所指向元素的大小关系）
  • 在查找表升序排列的情况下，若给定值key大于中间元素则所查找的元素只可能在后半部分。此时让low=mid+1；
  • 若给定值key小于中间元素则所查找的元素只可能在前半部分。此时让high=mid-1；

查找的效率分析

• 对于给定序列7-10-13-16-19-29-32-33-37-41-43
  

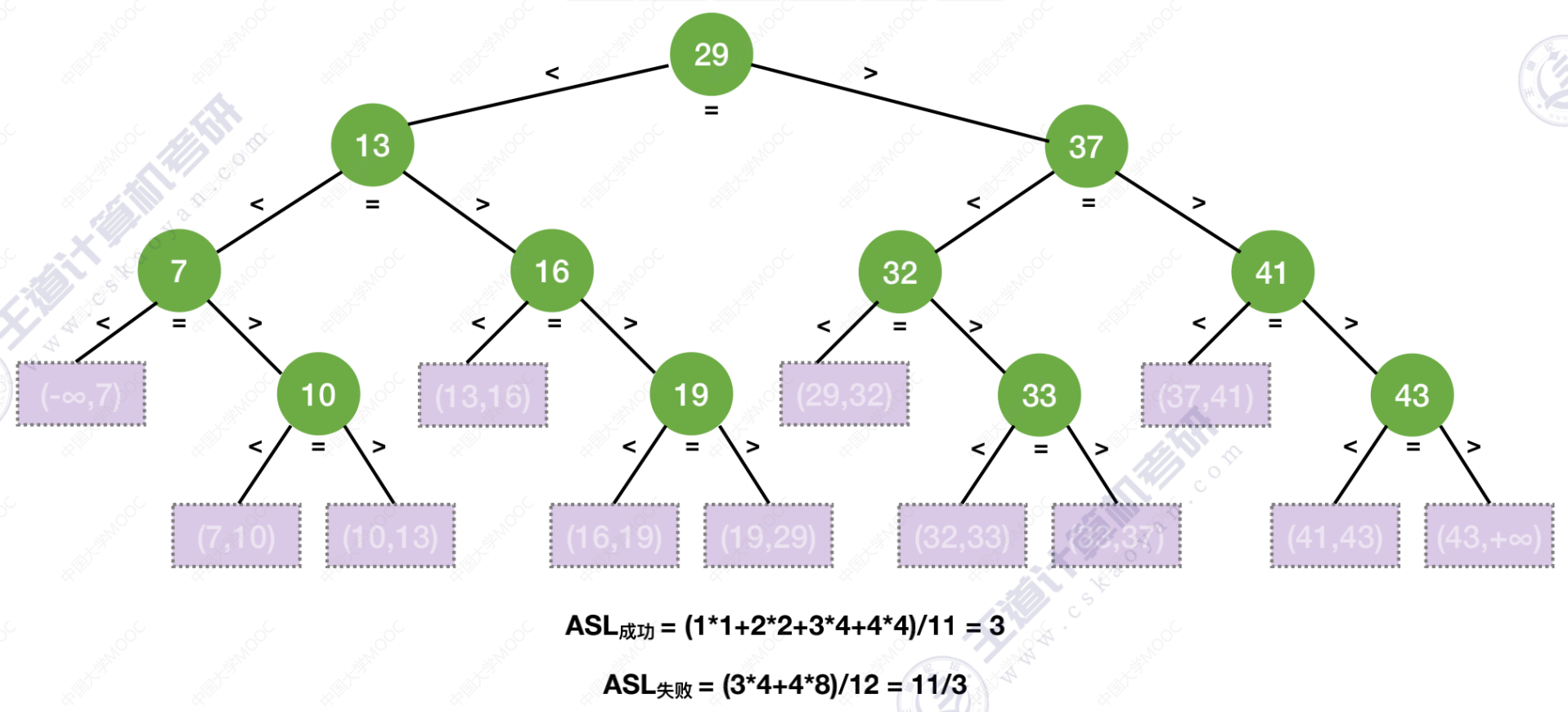
折半查找判定树的构造 –> mid =⌊(low + high) / 2⌋

• 如果当前low和high之间有奇数个元素,则mid分隔后，左右两部分元素个数相等 。
  
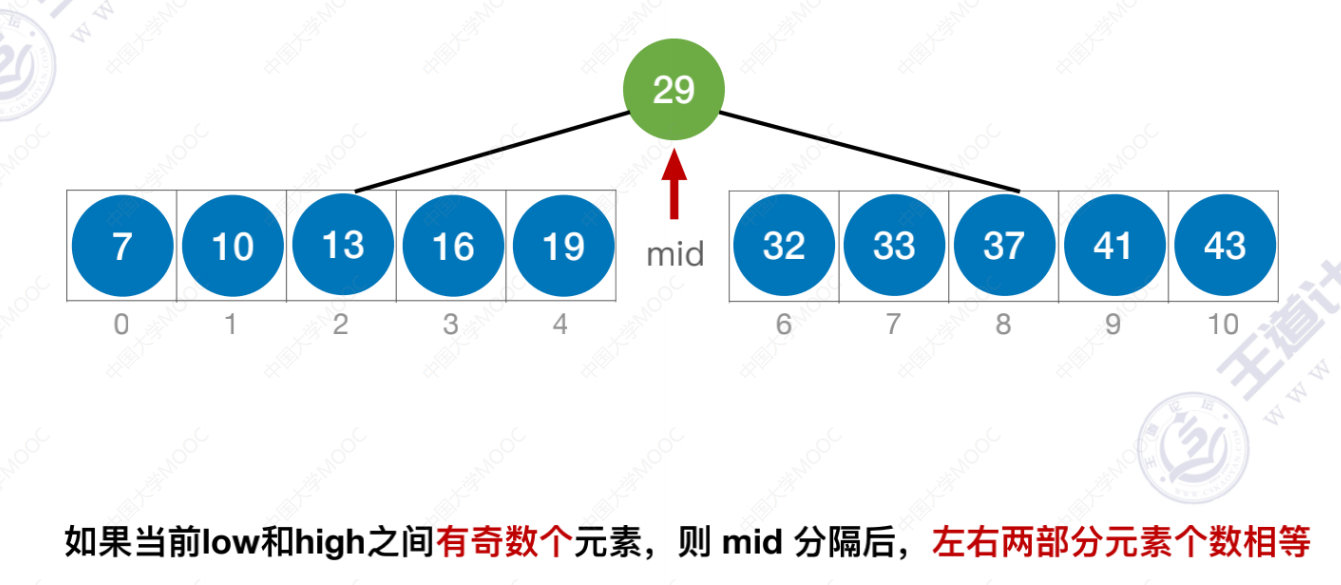
• 如果当前low和high之间有偶数个元素,则mid分隔后，左半部分比右半部分少一个元素 。
  
• 折半查找判定树中，若mid =⌊(low + high) / 2⌋，则对于任何一个结点，必有：右子树结点数 - 左子树结点数 = 0 或 1
  
• 折半查找的判定树一定是平衡二叉树
  
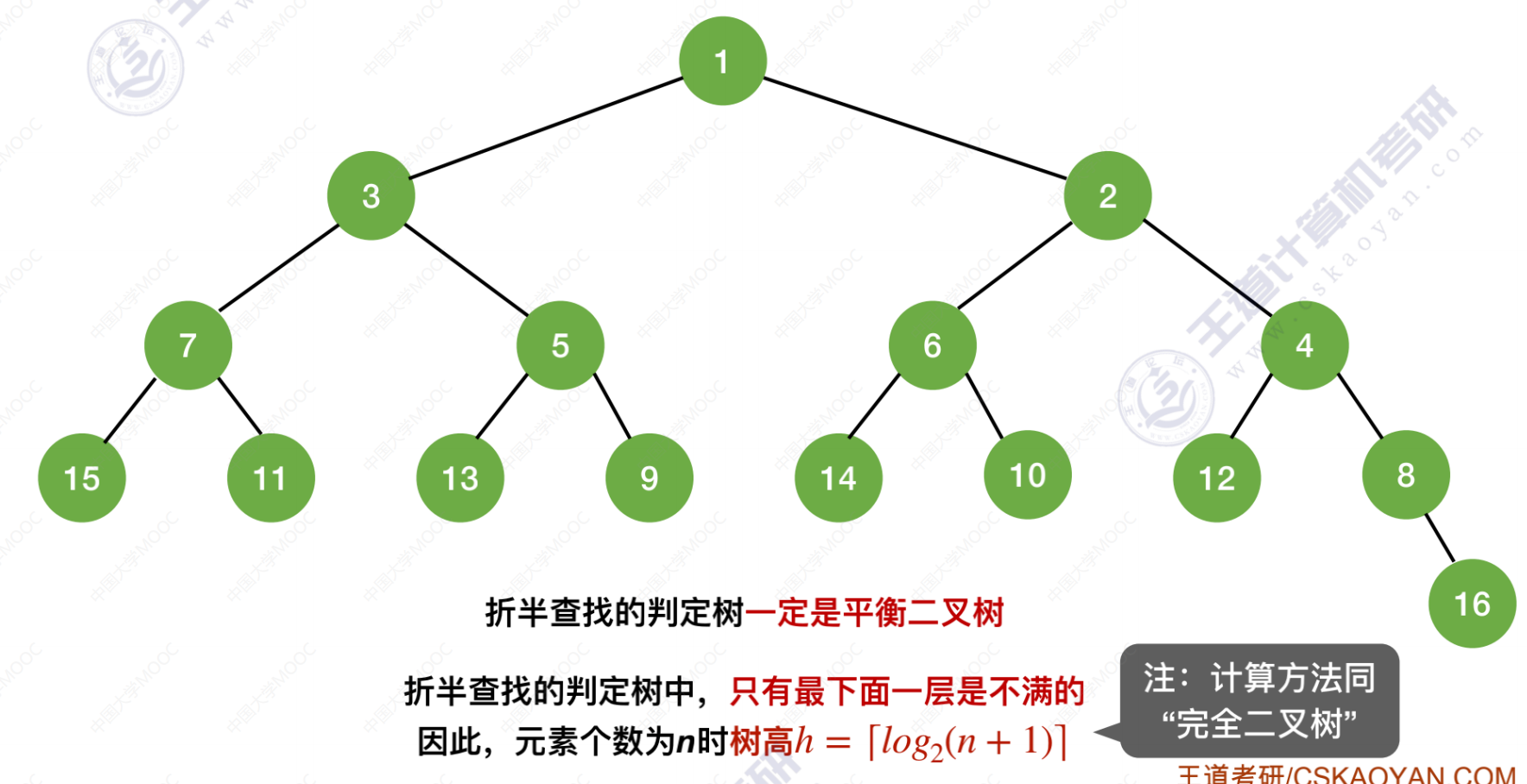
• 判定结点关键字：左 < 根 < 右，满足二叉排序树的定义 —> 失败结点：n + 1 (等于成功结点的空链域数)
  

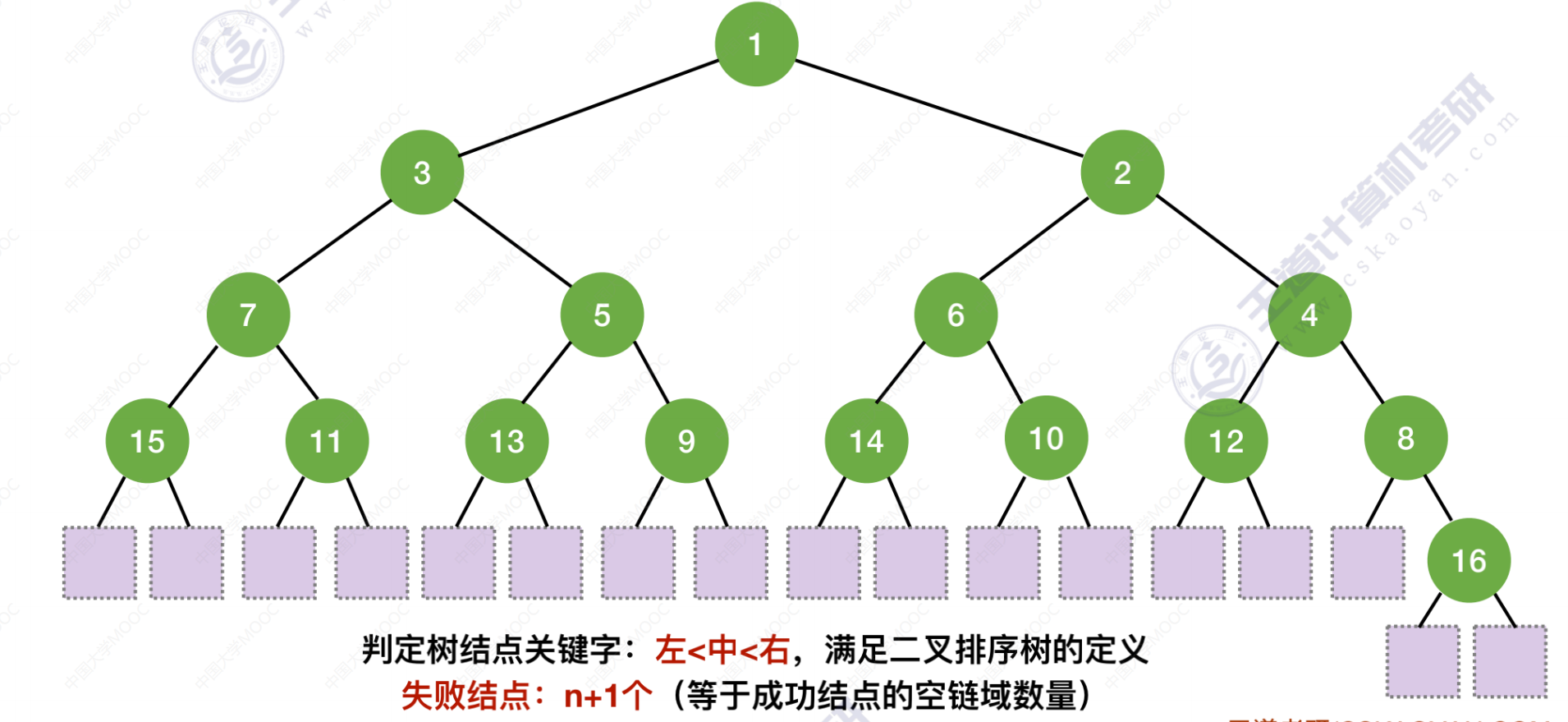
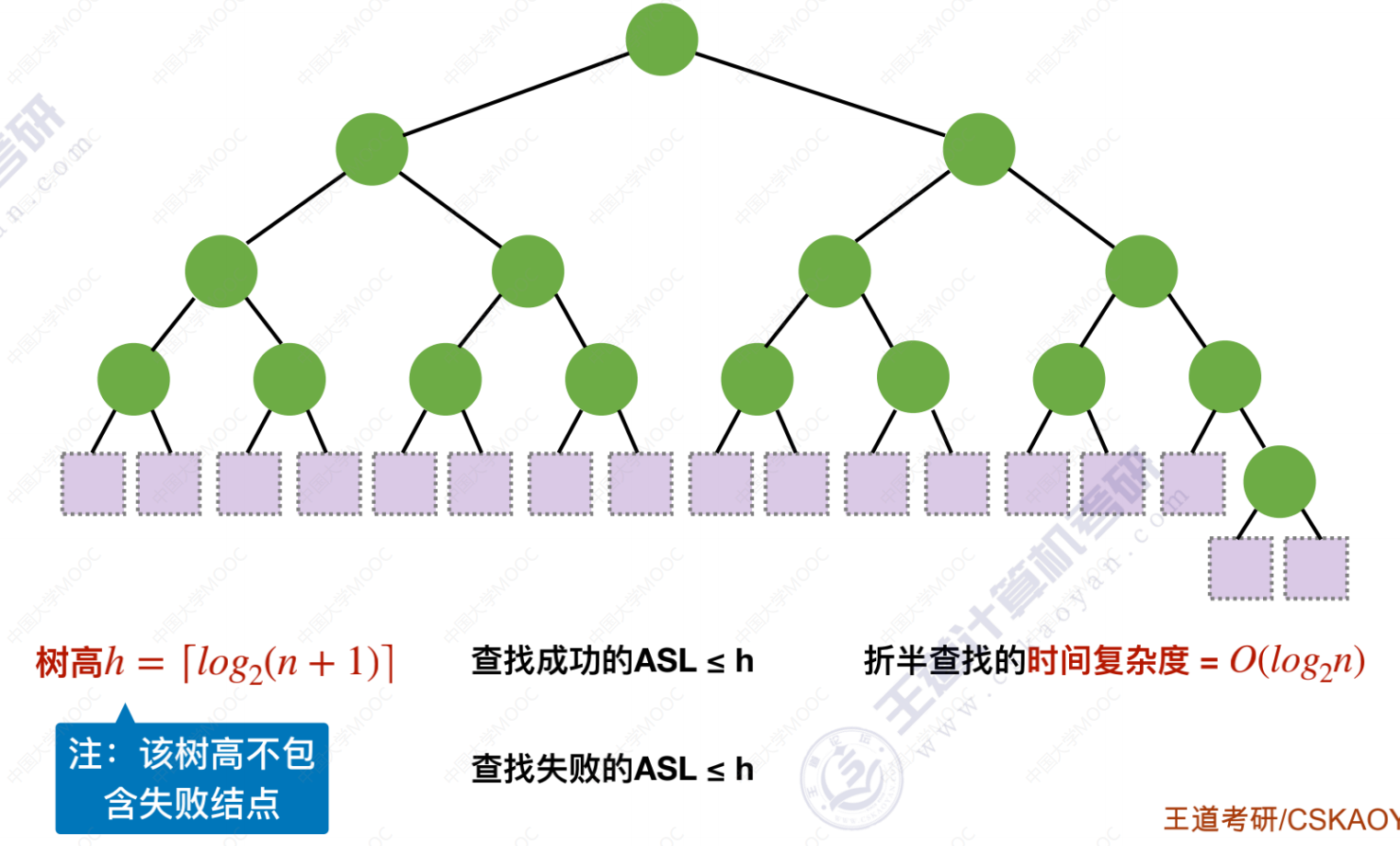
折半查找的查找效率

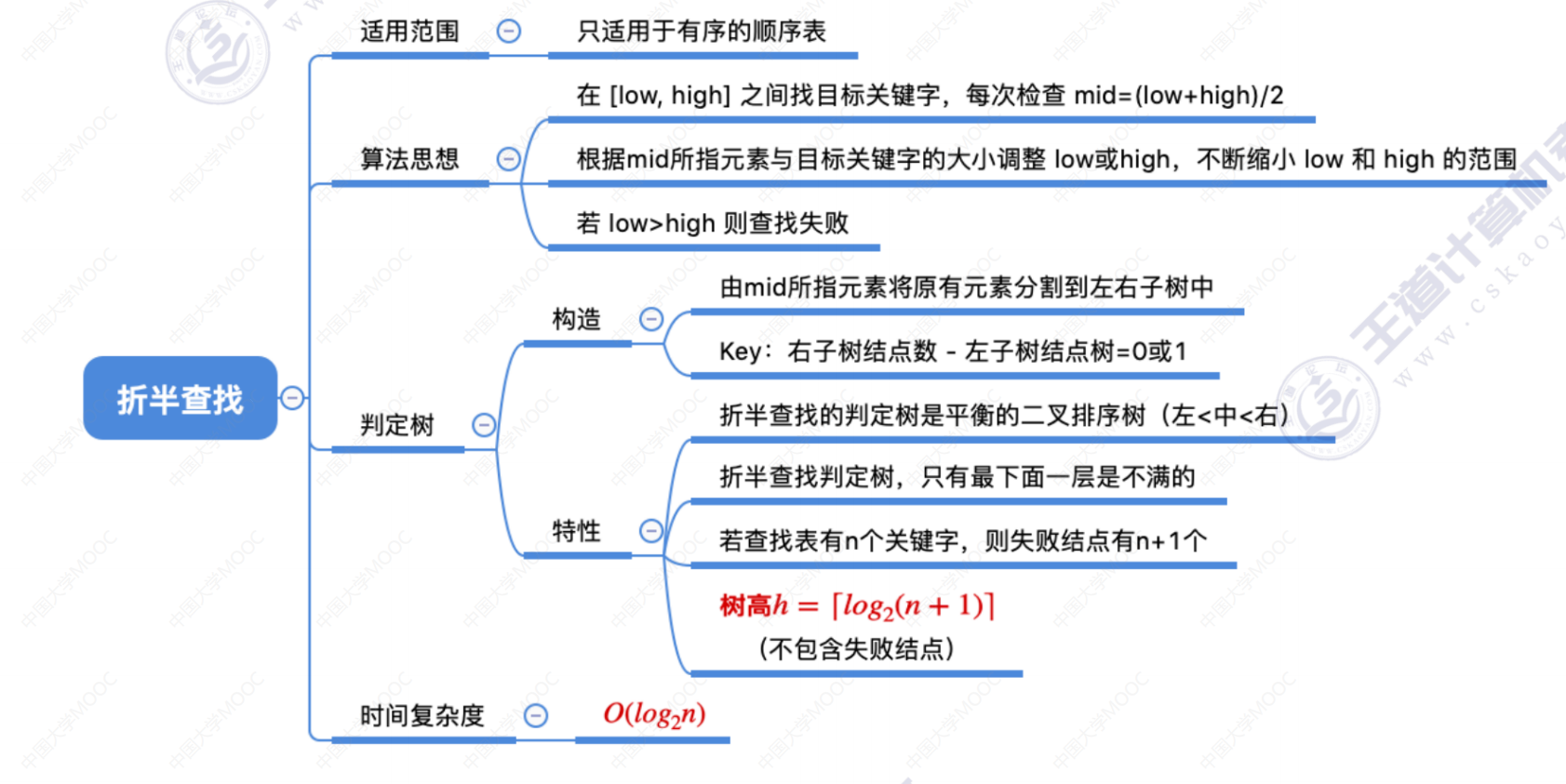
总结

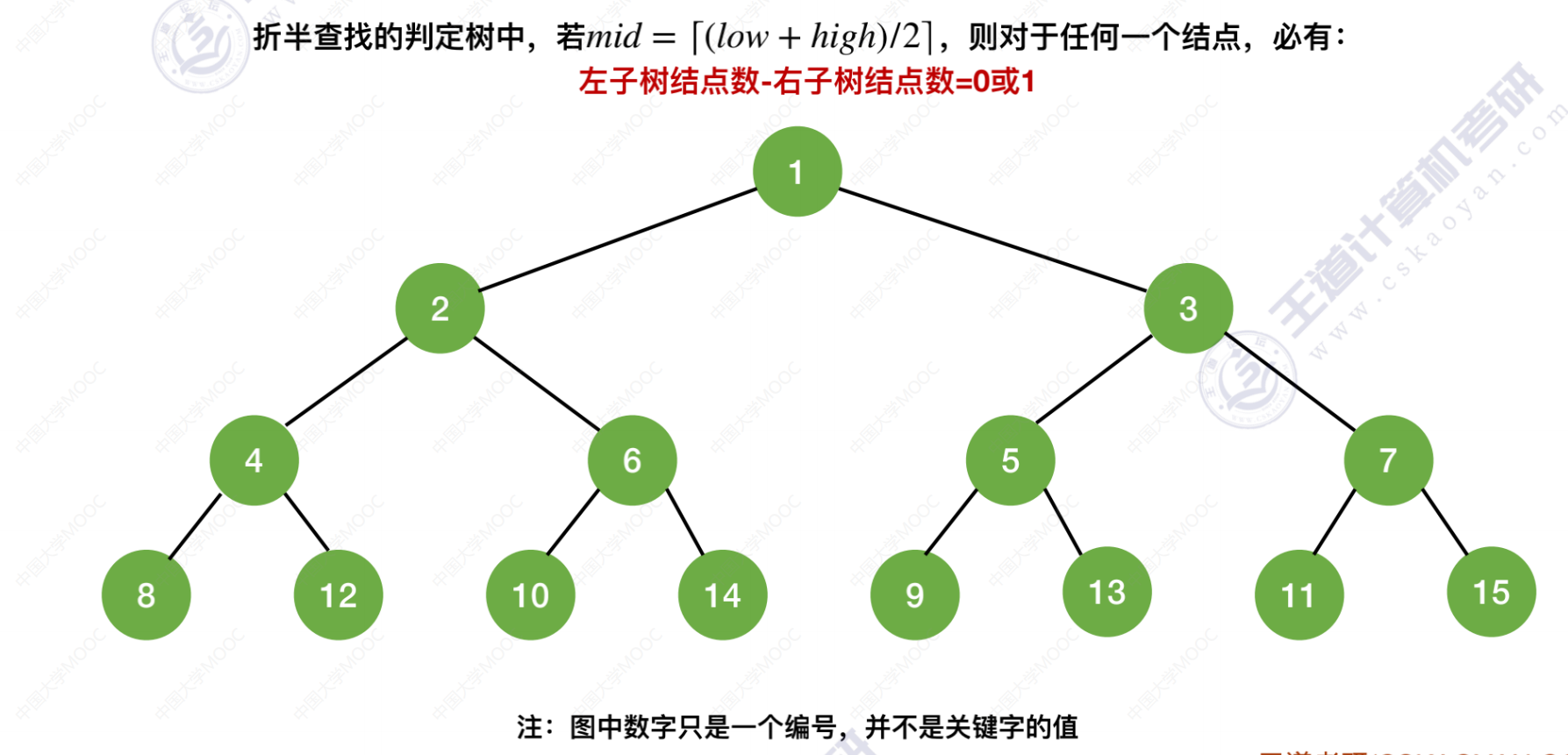
拓展 –> 如果mid = ⌈(low + high) / 2⌉

• 如果当前low和high之间有奇数个元素,则mid分隔后，左右两部分元素个数相等 。
  
• 如果当前low和high之间有偶数个元素,则mid分隔后，左半部分比右半部分多一个元素 。
  
• 折半查找判定树中，若mid = mid = ⌈(low + high) / 2⌉，则对于任何一个结点，必有：左子树结点数 - 右子树结点数 = 0 或 1