外部排序

算法思想

1. 外部排序：数据元素太多，无法一次全部读入内存进行排序
2. 使用归并排序的方法，最少只需在内存中分配3块大小的 缓冲区即可对任意一个大文件进行排序
3. 若要进行k路归并排序，则需要在内存中分配k个输入缓冲区和1个输出缓冲区
4. 步骤
   1. 生成r个初始归并段(对L个记录进行内部排序，组成一个有序的初始归并段)
   2. 进行S趟k路归并，S = [ log_k^r ] (向上取整)
5. 如何进行k路归并
   1. 把k个归并段的块读入k个输入缓冲区
   2. 用“归并排序”的方法从k个归并段中选出几个最小的记录暂存到输出缓冲区中
   3. 当输出缓冲区满时，写出外存
6. 外部时间开销：
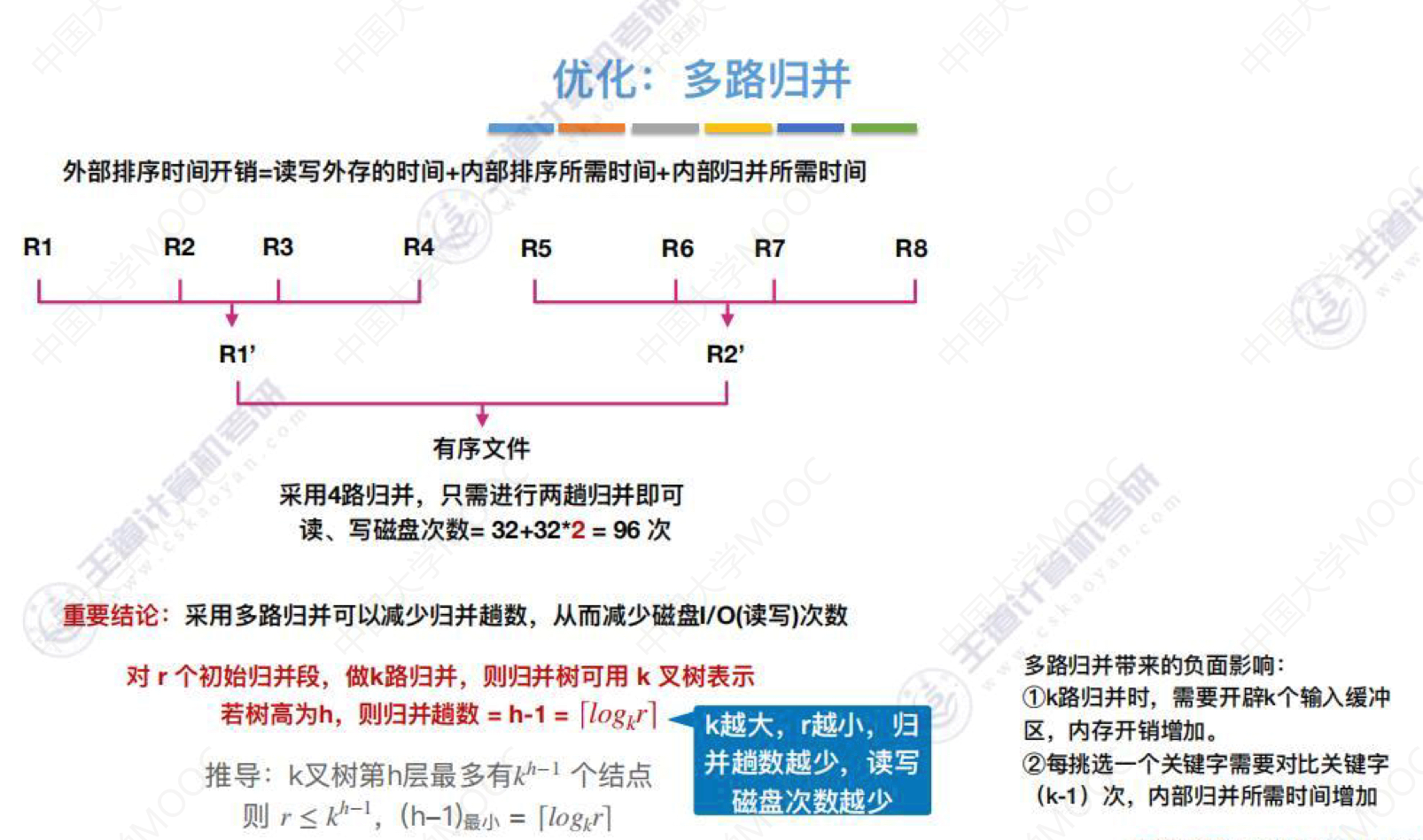
   ※ 读写外存时间 + 内部排序所需时间 + 内部归并所需时间
7. 优化：
   1. 增加归并路数k，进行多路平衡归并
      ※ 代价1：需要增加相应的输入缓冲区
      ※ 代价2：每次从k个归并段中选一个最小元素需要(k-1)次关键字对比
   2. 减少初始归并段数量r
8. k路平衡归并
   1. 最多只能有k个段归并为一个
   2. 每一趟归并中，若有m个归并段参与归并，则经过这一趟处理得到[ m/k ] (向上取整) 个新的归并段
9. 重要结论：
10. 

败者树

重要思想

1. 多路平衡归并带来的问题
   
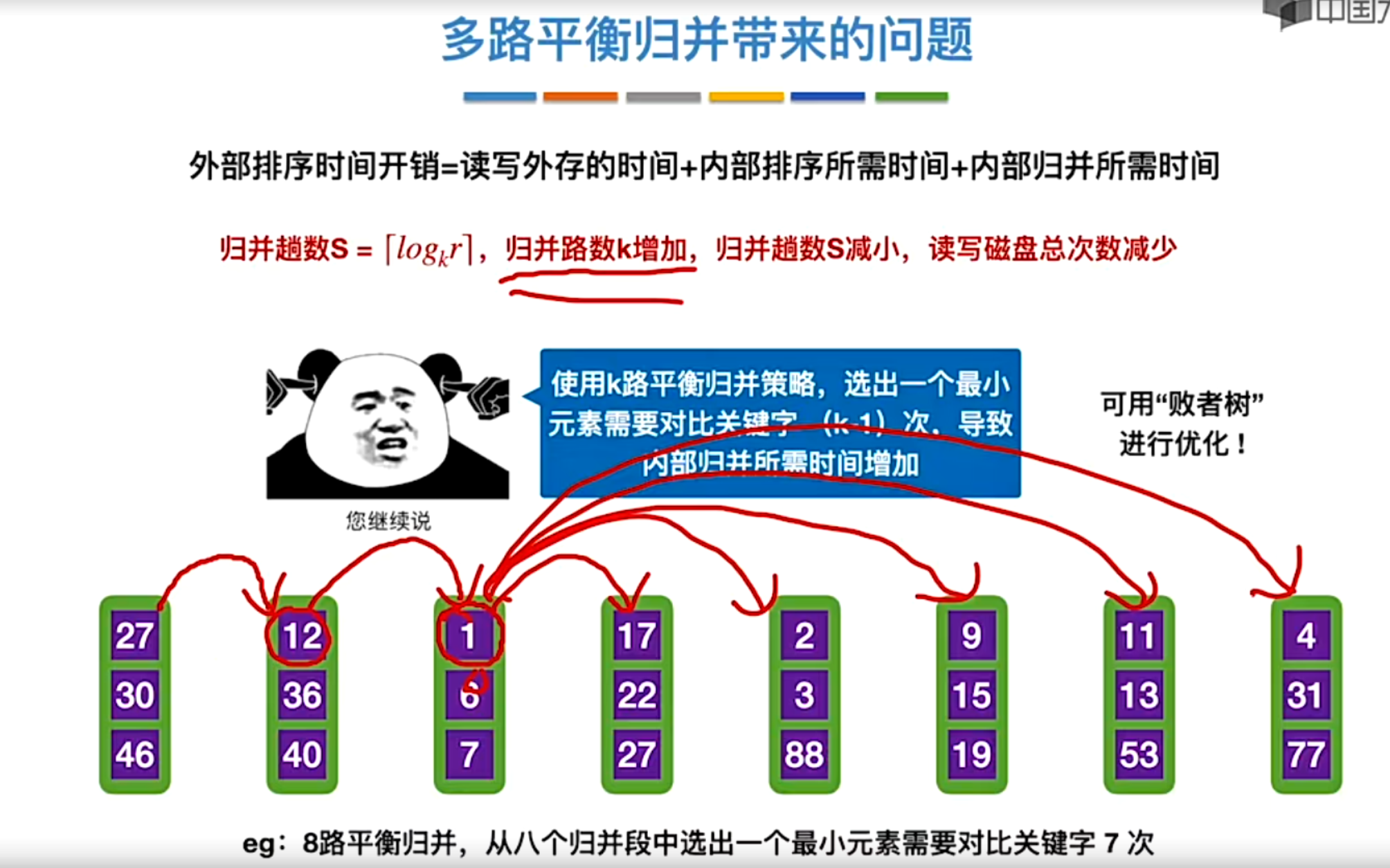
2. 什么是败者树
   可视为一颗完全二叉树（多了一个头头）。k个叶结点分别是当前参加比较的元素，非叶结点用来记录左右子树中的“失败者”，而让胜者往上继续进行比较，一直到根节点
3. 败者树在多路平衡归并中的应用
   1. 对于k路归并，第一次构造败者树需要对比关键字k-1次
   2. 有了败者树，选出最小元素，只需要对比关键字[ log₂^k ] (向上取整)次

置换选择排序

重要思想

1. 由于内部排序的内存工作区WA可容纳L个记录，则每个初始归并段也只能包含L个记录，若文件共有n个记录，则初始归并段的数量r = n / L。
2. 算法执行过程
   

最佳归并树

重要思想

1. 归并树
   
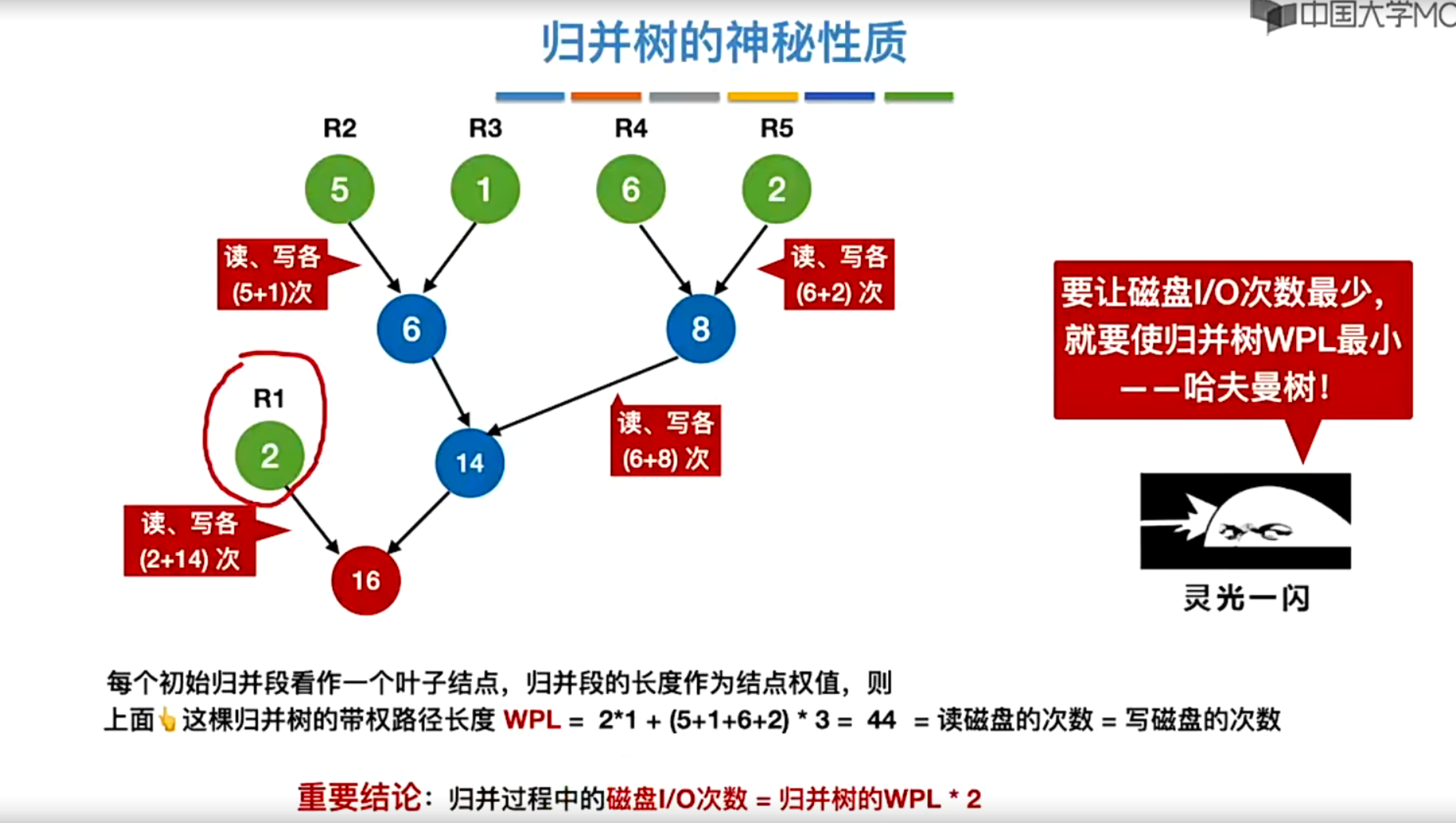
2. 构造2路归并的最佳归并树
   
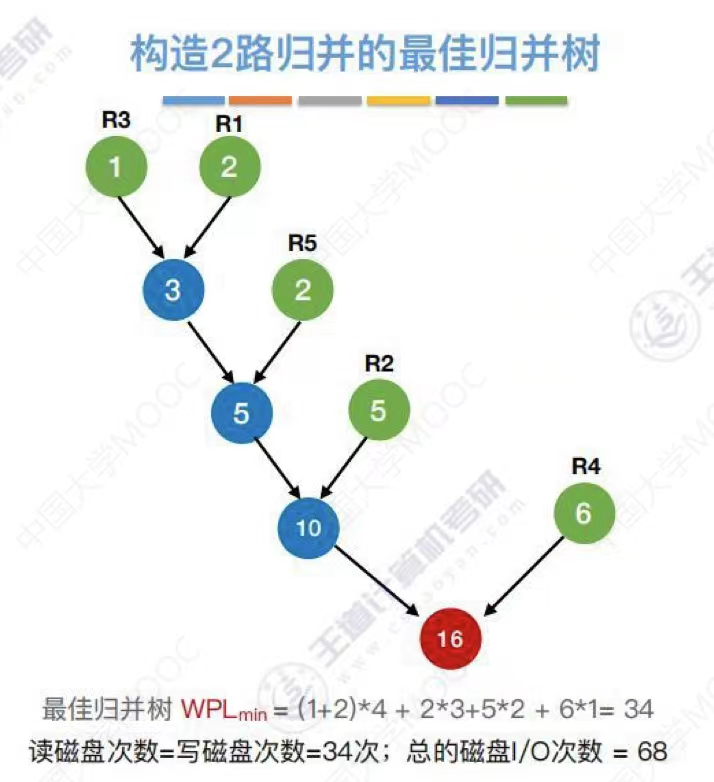
3. 多路归并
   
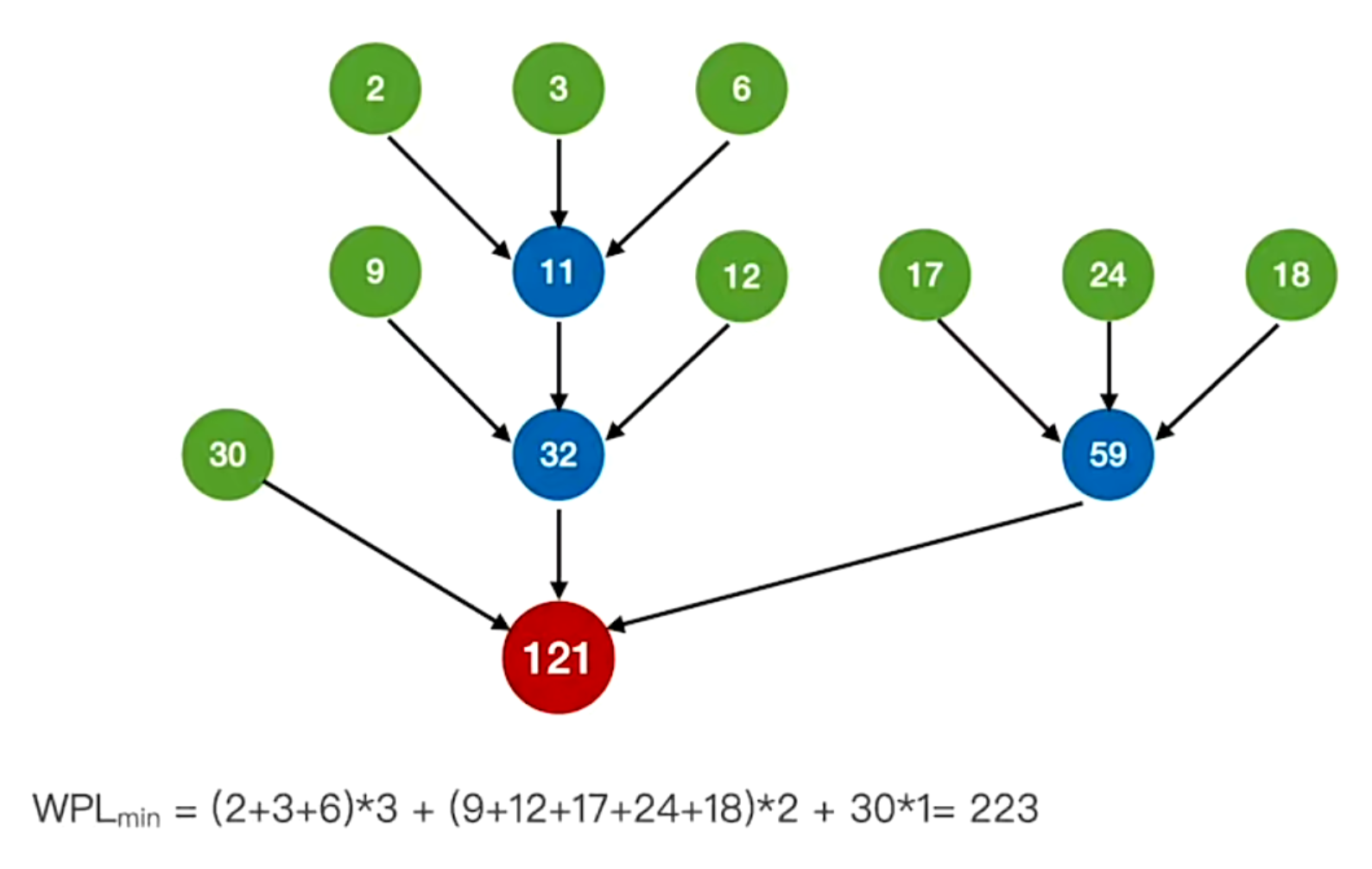
4. 注意 ——> 对于k叉归并，若初始归并段的数量无法构成严格的k叉归并树，则需要补充几个长度为0的“虚段”，再进行k叉哈夫曼树的构造
   
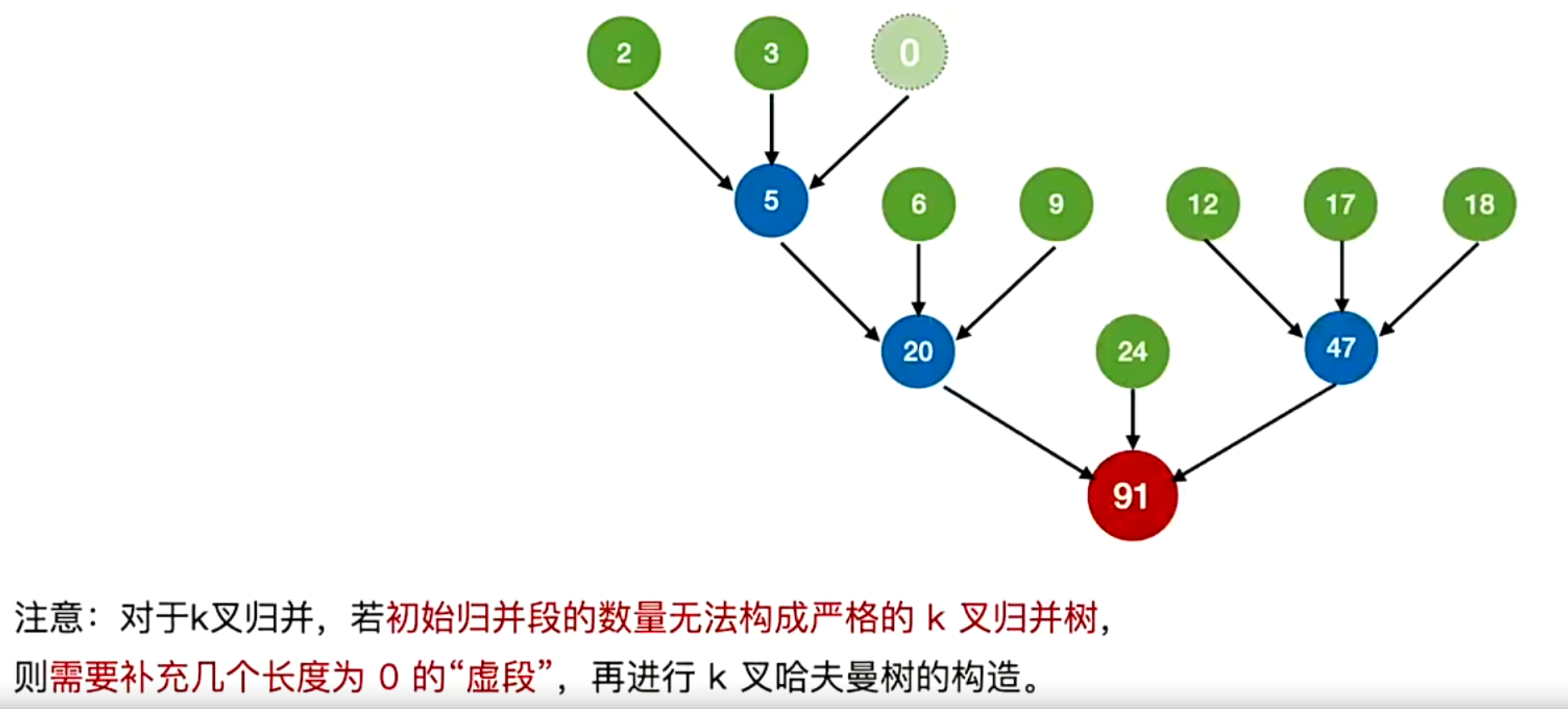
5. 添加虚段的数量
   

题目总结

1. 置换-选择排序是外部排序中生成初始归并段的方法，用此方法得到的初始归并段的长度是不等长的，其长度平均是传统等长初始段的2倍，从而使得初始归并段数减少到原来的近二分之一。但是，置换-选择排序不是一种完整的生成有序文件的外部排序算法。
2. 最佳归并树在外部排序中的作用是设计m路归并排序的优化方案，仿照哈夫曼树的方法，以初始归并段的长度为权值，构造具有最小带权路径长度的m叉哈夫曼树，可以有效减少归并过程中的读写记录数，加快外部排序的速度。
3. 在外部排序过程中输入/输出缓冲区就是排序的内存工作区，例如做m路平衡归并需要m个输入缓冲区和1个输出缓冲区，用以存放参加归并的和归并完成的记录。在产生初始归并段时也可以作内部排序的工作区
4. 在做m路平衡归并排序的过程中，为实现输入/输出的并行处理，需要设置2m个输入缓冲区和2个输出缓冲区，以便在执行内部归并时，能同时进行输入/输出操作。若仅设置m个缓冲区，则仅能进行串行操作，无法并行处理。