选择排序

选择排序

简单选择排序

算法思想

假设排序表为L[1…n],第i趟排序即L[i…n]中选择关键字最小的元素与L(i)交换，每一趟排序可以确定一个元素的最终位置，这样经过n - 1 趟排序就可使得整个排序表有序。

模板代码

1
2
3
4
5
6
7
8
void SelectSort(ElemType A[],int n){
    for(int i = 0;i < n - 1;i ++){              //一共进行 n - 1 趟
        int min = i;                            //记录最小元素的位置
        for(int j = i + 1;j < n;j ++)           //在A[i...n-1]中选择最小的元素
            if(A[j] < A[min]) min = j;          //更新最小元素的位置
        if(min != i) swap(A[i],A[min]);         //封装的swap()函数共移动3次
    }
}

性能分析

  1. 空间效率：仅使用常数个辅助单元，故空间效率为O(1).
  2. 时间效率：从上述伪代码中不难看出，在简单选择排序过程中，元素移动的操作次数很少，不会超过3(n - 1)次，最好的情况是移动0次，此时对应的表已有序；但元素比较的次数与序列的初始状态无关，始终是 n(n - 1) / 2 次，因此时间复杂度始终是O(n2)。
  3. 稳定性：简单选择排序是一种不稳定的排序方法。

堆排序

算法思想

  1. 堆的定义：
    若n个关键字序列L[1…n]满足下面某一条性质，则称为堆(Heap)
    ①若满足：L(i) >= L(2i) 且L(i) >= L(2i + 1) ( 1 <= i <= n/2)—-> 大根堆(大顶堆) 根>左>右。
    ②若满足：L(i) <= L(2i) 且L(i) <= L(2i + 1) ( 1 <= i <= n/2)—-> 小根堆(小顶堆)。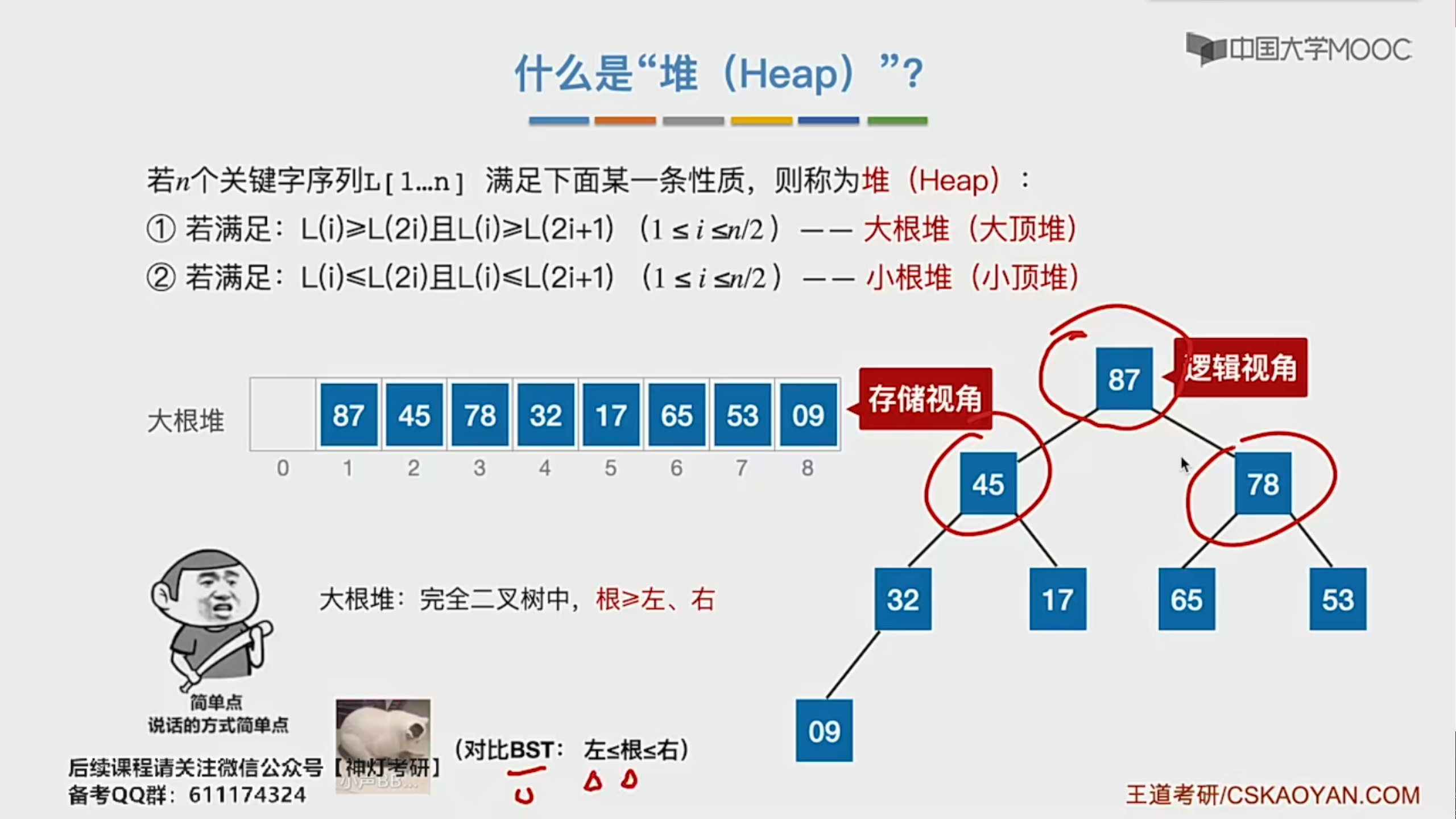
  2. 大根堆的建立
    1. 思路：把所有非终端结点都检查一遍(从后往前扫描)，是否满足大根堆的要求，如果不满足，则进行调整
    2. 在顺序存储的完全二叉树中，非终端结点编号为i <= [n/2] 向下取整
    3. i的左孩子—–> 2i
      i的右孩子—–> 2i + 1
      i的父节点—–> [i/2] 向下取整
    4. 检查当前结点是否满足 根 >= 左、右。若不满足，将当前结点与更大的一个孩子互换。
    5. 若元素互换破坏了下一级的堆，则应采用相同的方式继续往下调整(小元素不断“下坠”)
  3. 堆排序
    1. 每一趟将堆顶元素加入有序子序列(与待排序序列中的最后一个元素交换)
    2. 并将待排序元素序列再次调整为大根堆(小元素不断“下坠”)
    3. 基于“大根堆”的堆排序得到“递增序列”
    4. 基于“小根堆”的堆排序得到“递减序列”
  4. 在堆中插入新元素
    1. 对于小根堆，新元素放到表尾，与父节点对比，若新元素比父节点更小，则将二者互换。新元素就这样一路“上升”，直到无法继续上升为止。
  5. 在堆中删除元素
    1.被删除的元素用堆底元素替代，然后让该元素不断“下坠”，直到无法下坠为止。

模板代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//建立大根堆
void BuildMaxHeap(int A[],int len){
    for(int i = len / 2;i > 0;i --)
    HeadAdjust(A,i,len);
}

//将以 k 为根的子树调整为大根堆
void HeadAdjust(int A[],int k,int len){
    A[0] = A[k];                        //A[0]暂存子树的根结点
    for(int i = 2 * k;i <= len;i *= 2){ //沿key较大的子结点向下筛选
        if(i <len && A[i] < A[i + 1])
            i++;                        //取key较大的子结点的下表
        if(A[0] > A[i]) break;          //筛选结束
        else{
            A[k] = A[i];
            k = i;                      //修改k值，以便继续向下筛选
        }
    }
    A[k] = A[0];                        //被筛选结点的值放入最终位置
}

//堆排序的完整逻辑
void HeapSort(int A[],int len){
    BuildMaxHeap(A,len);                //初始建堆
    for(int i = len;i > 1;i --){        //n-1趟的交换和建堆的过程
        swap(A[i],A[1]);                //堆顶元素和堆底元素交换
        HeadAdjust(A,1,i - 1);          //把剩余的待排序元素整理成堆
    }
}

性能分析

  1. 建堆的过程，关键字对比次数不超过4n，建堆时间复杂度 = O(n)。
  2. 空间效率：仅使用了常数个辅助单元，所以空间复杂度为O(1).
  3. 时间效率：建堆时间为O(n),之后有n-1次向下调整操作，每次调整的时间复杂度为O(h),故在最好、最坏和平均情况下，堆排序的时间复杂度为O(nlog2n)。
  4. 稳定性：进行筛选时，有可能把后面相同关键字的元素调整到前面，所以堆排序算法是一种不稳定的排序算法。

题目总结

  1. 简单选择排序算法的比较次数为O(n2),移动次数为O(n).
  2. 小根堆关键字最大的记录一定存储在这个堆所对应的完全二叉树的叶结点中；又因为二叉树中的最后一个非叶结点存储在n/2中，所以关键字最大记录的存储范围为[n/2] + 1 ~ n。
  3. 向具有n个结点的堆中插入一个新元素的时间复杂度为O(log2n),删除一个元素的时间复杂度为O(log2n)。
  4. 构建n个记录的初始堆，其时间复杂度为O(n);对n个记录进行堆排序，最坏情况下其时间复杂度为O(nlog2n)。
  5. 堆中输出两个最小关键码 ——-> 说明是小根堆
  6. 选择排序算法的比较次数始终为n(n-1)/2,与序列初始状态无关
数据结构 > 第八章 排序
选择排序
https://lzyjx.github.io.git/2023/05/10/选择排序/
作者
六只羊
发布于
2023年5月10日
许可协议