Trie

Trie数

Tire树介绍

1. Tire 树 又称单词查找树，是一种树形结构，是一种哈希树的变种。
2. Tire 树是一种能够快速存储和查找一组字符串集合的数据结构，是以空间换时间，利用字符串的前缀来降低查询时间。
3. 与二叉树不同，Tire 树有 26 子节点对应 26 个字母，根节点不包含字符串，从根节点到某个节点，经过的字符连起来的字符串就是对应的字符串。当储存结束一个字符串后，尾节点会产生一个标记，表示当前字符串已经结束了。
4. 典型应用：用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。
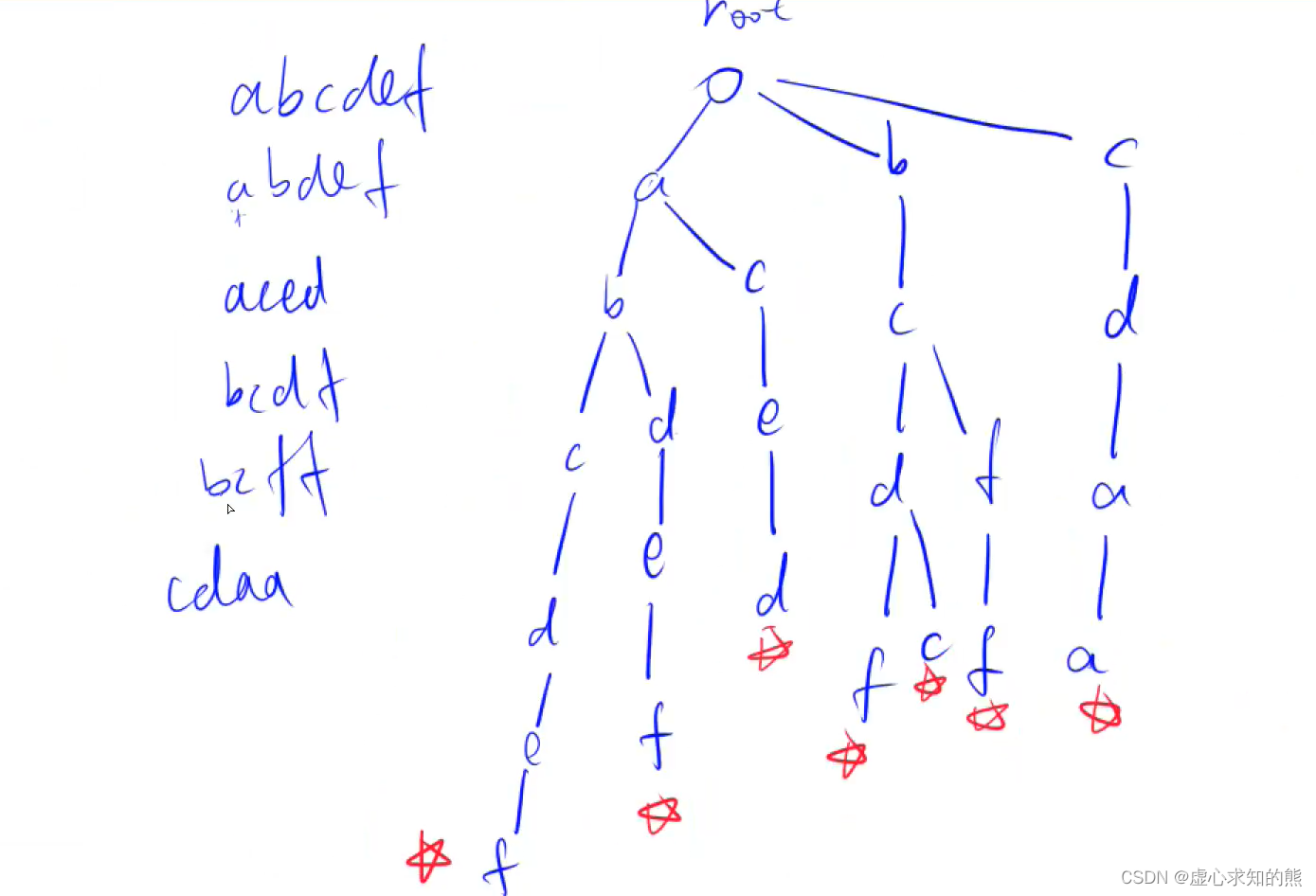
5. 如下图就是一棵由字符串 abcdef，abdef，aced，bcdf，bcfc，bcff，cdaa，组成的 Tire 树：
   

优缺点及性质

1. 优点：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。
2. 缺点：空间复杂度比较大。
3. 优化：我们可以用链表来动态开辟空间，达到空间上利用率的最大化。
4. 性质：

（1）根结点不包含字符，其他的每一个节点只包含一个字符。

（2）从根结点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串（假如某个节点为一个字符串的结尾，对其打个标记即可）。

（3）每个节点的所有子节点包含的字符都不相同。

Tire树例题—->Tire字符串统计

完整代码

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int son[N][26],cnt[N],idx;      //son[N][26]:储存子节点的位置，分支最多26条,cnt[N]表示以当前这个点结尾的单词有多少个，idx表示当前用到了哪个下标，下标是0的点，既是根节点，又是空节点
char str[N];
void insert(char str[]){
    int p = 0;      //从根节点出发
    for(int i = 0;str[i];i ++){
        int u = str[i] - 'a';           //当前节点是什么字符
        if(!son[p][u]) son[p][u] = ++ idx;  //如果节点不存在就新建节点
        p = son[p][u];      //p指向新建的节点
    }
    cnt[p] ++;      //表示以这个字母结尾的单词增加了一个
}

int query(char str[]){
    int p;
    for(int i = 0;str[i];i ++){
        int u = str[i] - 'a';
        if(!son[p][u])  return 0;       //该节点不存在，即该字符串不存在
        p = son[p][u];
    }
    return cnt[p];      //返回字符串出现的次数
}

int main(){
    int n;
    scanf("%d",&n);
    while(n -- ){
        char op[2];
        scanf("%s%s",op,str);
        if(op[0] == 'I') insert(str);
        else printf("%d\n", query(str));
    }
    return 0;
}

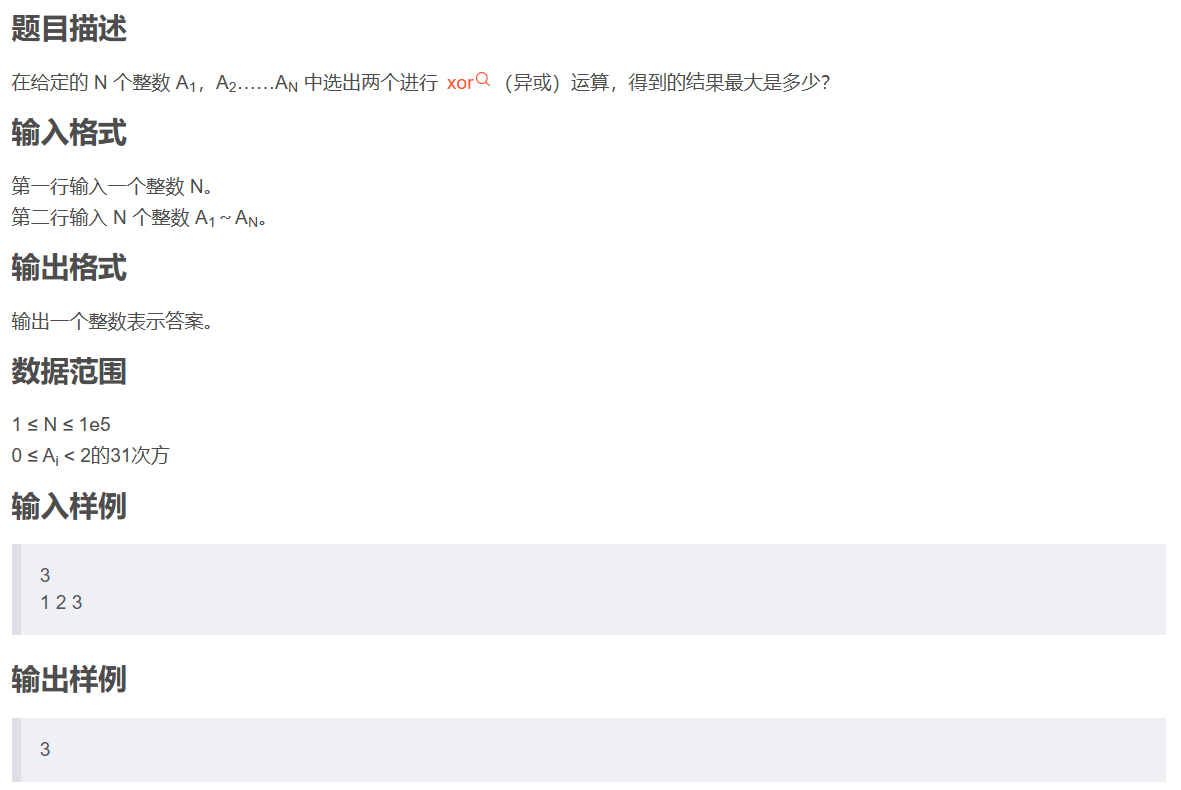
Tire树例题—–>最大异或对

暴力做法

1. 暴力做法通俗易懂，两个 for 循环，相互枚举每一个值，异或，最后答案为其中的最大值。
2. 暴力做法虽然易做，但是会出现 超时 问题。

完整代码

#include <bits/stdc++.h>
using namespace std;

const int N=100010;
int n;
int a[N];
int main()
{
	cin>>n;
	for(int i=0;i<n;i++)
	{
		cin>>a[i];
	}
	int res=0;
	for(int i=0;i<n;i++)
	{
		for(int j=0;j<n;j++)
		{
			res=max(res,a[i]^a[j]);
		}
	}
	cout<<res<<endl;
	system("pause"); 
	return 0;
}

优美解法

1. 首先，需要搞清楚 异或操作。
2. 如果 A = 1101 ，B = 0111，那么 A ^ B = 1010。详细讲解请见 基础算法-位运算
3. 对暴力做法进行优化，使其满足时间限制。
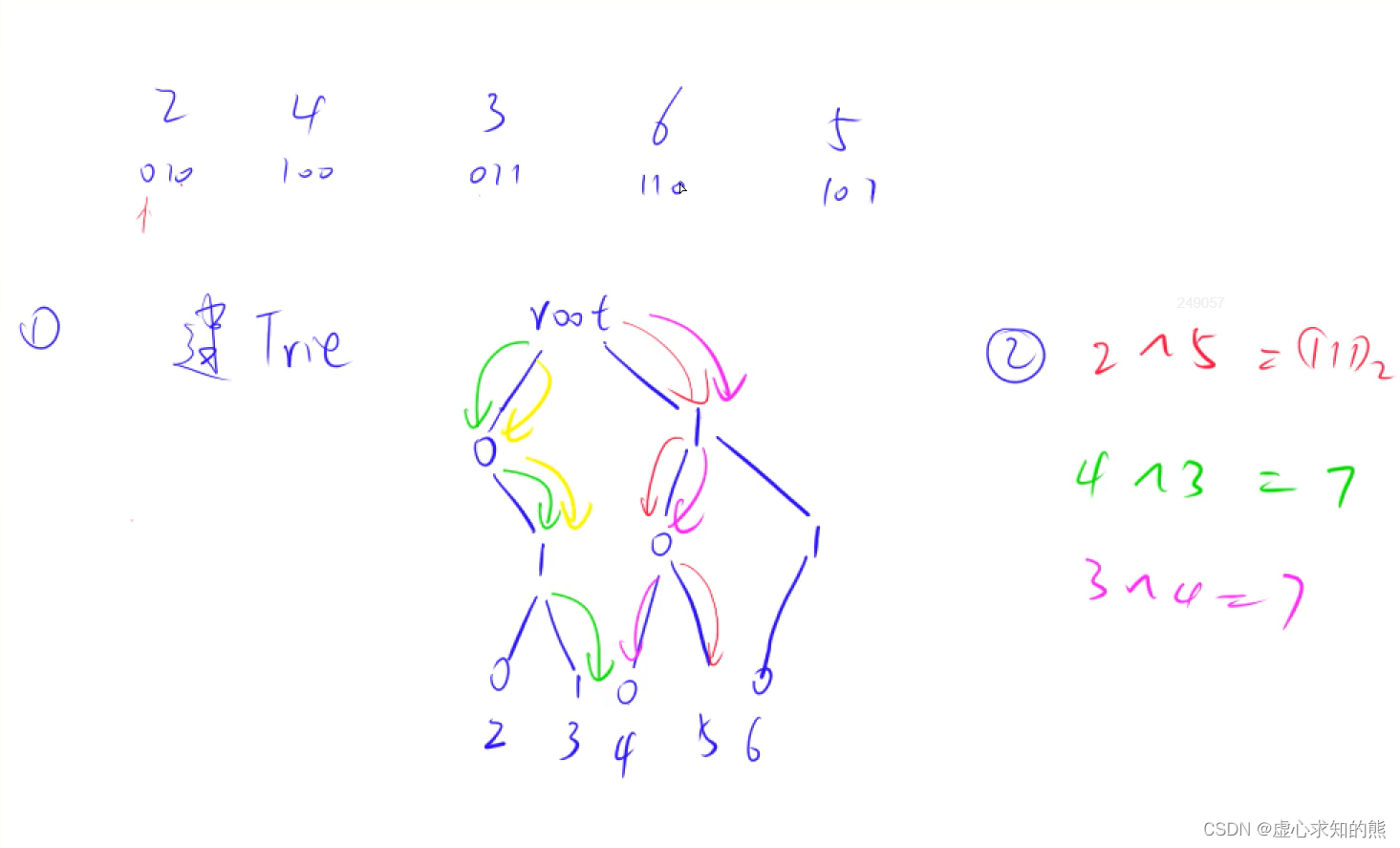
4. 由异或操作的计算公式可知，我们只需要先遍历每一个数，然后根据遍历的数的对应二进制形式，选取一个尽可能二进制形式每一位都不同的数字，得到该数字的最大异或值，最后再选举最大的异或值。在得到每一个数字的最大亦或值的选取过程就是一个 Tire 数。
5. 举例说明：
   

完整代码

#include <bits/stdc++.h>
using namespace std;

const int N = 100010, M = 3100010;
int n;
int a[N], son[M][2], idx;

void insert(int x)
{
    int p = 0;
    for (int i = 30; i >= 0; i -- )
    {
        int &s = son[p][x >> i & 1];
        if (!s) 
        {
            idx ++;
            s = idx;
        }
        p = s;
    }
}

int search(int x)
{
    int p = 0, res = 0;
    for (int i = 30; i >= 0; i -- )
    {
        int s = x >> i & 1;
        if (son[p][!s])
        {
            res += 1 << i;
            p = son[p][!s];
        }
        else 
        {
            p = son[p][s];
        }
    }
    return res;
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ )
    {
        cin >> a[i];
        insert(a[i]);
    }
    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        res = max(res, search(a[i]));
    }
    cout << res << endl;
    system("pause");
    return 0;
}