双指针算法

一个简单的例子

算法思想

输入一行字串如“abc def ghi”
将单词输出即
abc
def
ghi
※思路，定义两个指针，i指向第一个单词，j向后扫描，如果扫到’ ‘空格就停下来，然后输出i到j-1包含的单词，然后使i = j进入下一层循环。\

完整代码：

#include<iostream>
#include<string>
#include <cstring>
using namespace std;
int main(){
    char str[100];
    gets(str);
    int n = strlen(str);
    for(int i =0;i < n;i ++){
        int j = i;
        while(j < n && str[j] != ' ') j++;
        for(int k = i;k < j;k ++) cout << str[k];
        cout << endl;
        i = j;
    }
    return 0;
}

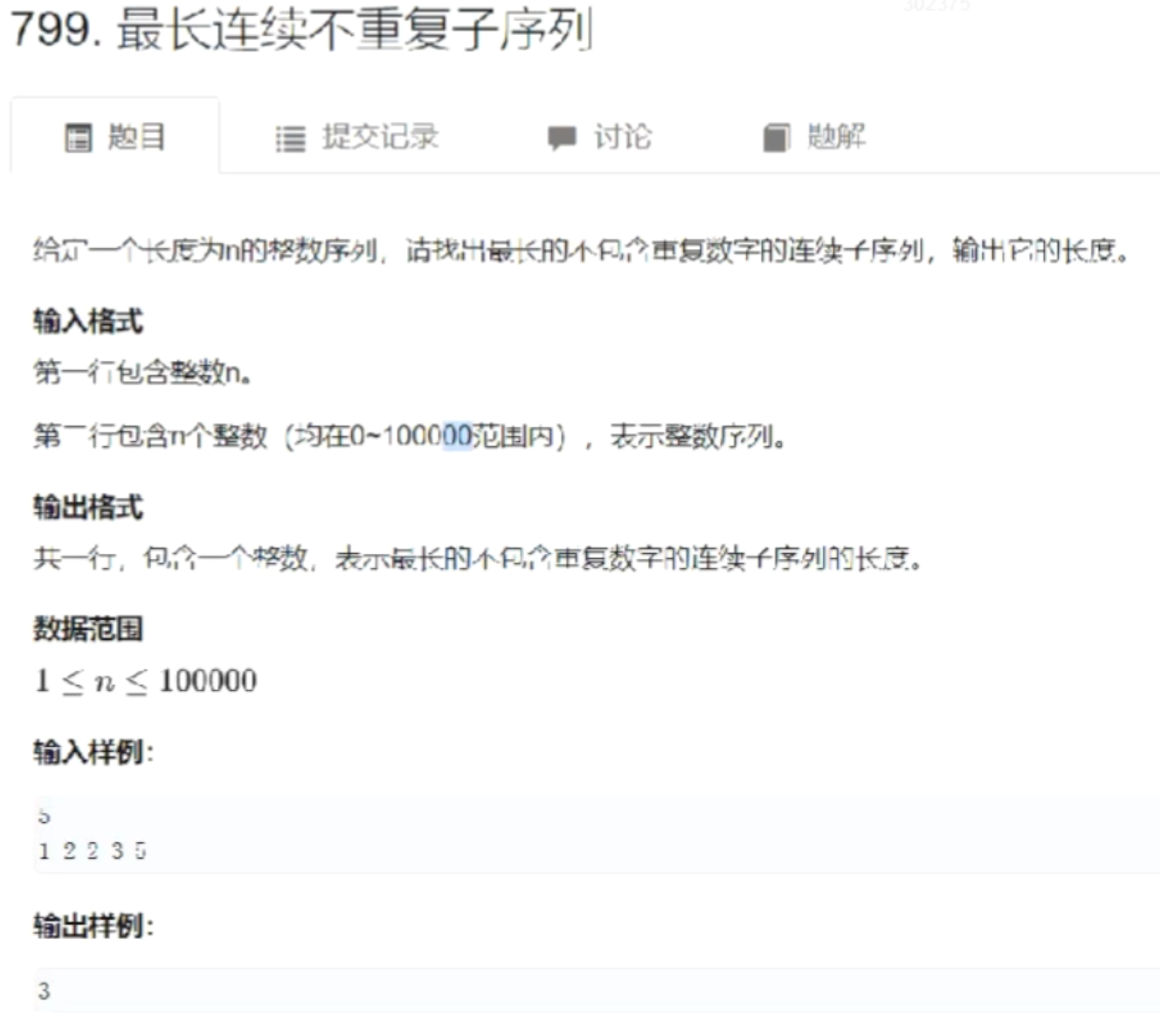
最长连续不重复子序列

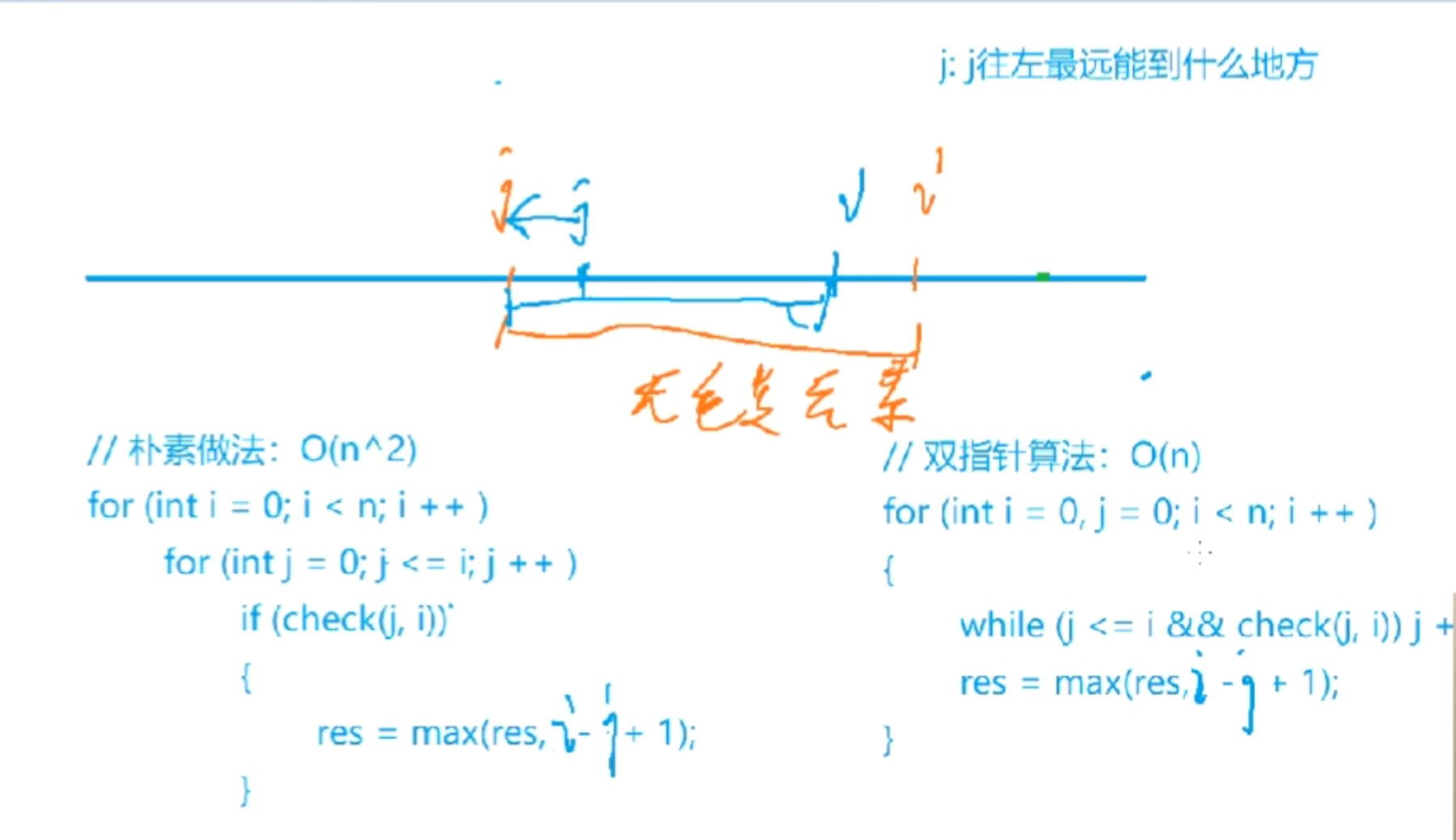
算法思想

※每次都枚举i,j从0开始。
※用s[]数组记录当前[j,i]中数的个数，当i前移时时s[a[i]]++，当s[a[i]] > 1时，说明区间内有重复的数，则让s[a[j]]–，然后使j往前移动，重复上述操作。
※不重复序列的长度res = max(res,i - j + 1)，因为i比j大

完整代码

#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N];
int s[N];
int n;

int main(){
    cin >> n ;
    for(int i = 0;i < n;i ++) scanf("%d",&a[i]);
    int res = 0;
    for(int i = 0,j = 0;i < n;i ++){
        s[a[i]] ++;
        while(s[a[i]] > 1){
            s[a[j]] --;
            j++;
        }
        res = max(res,i - j + 1);
    }
    cout << res << endl;
    return 0;
}

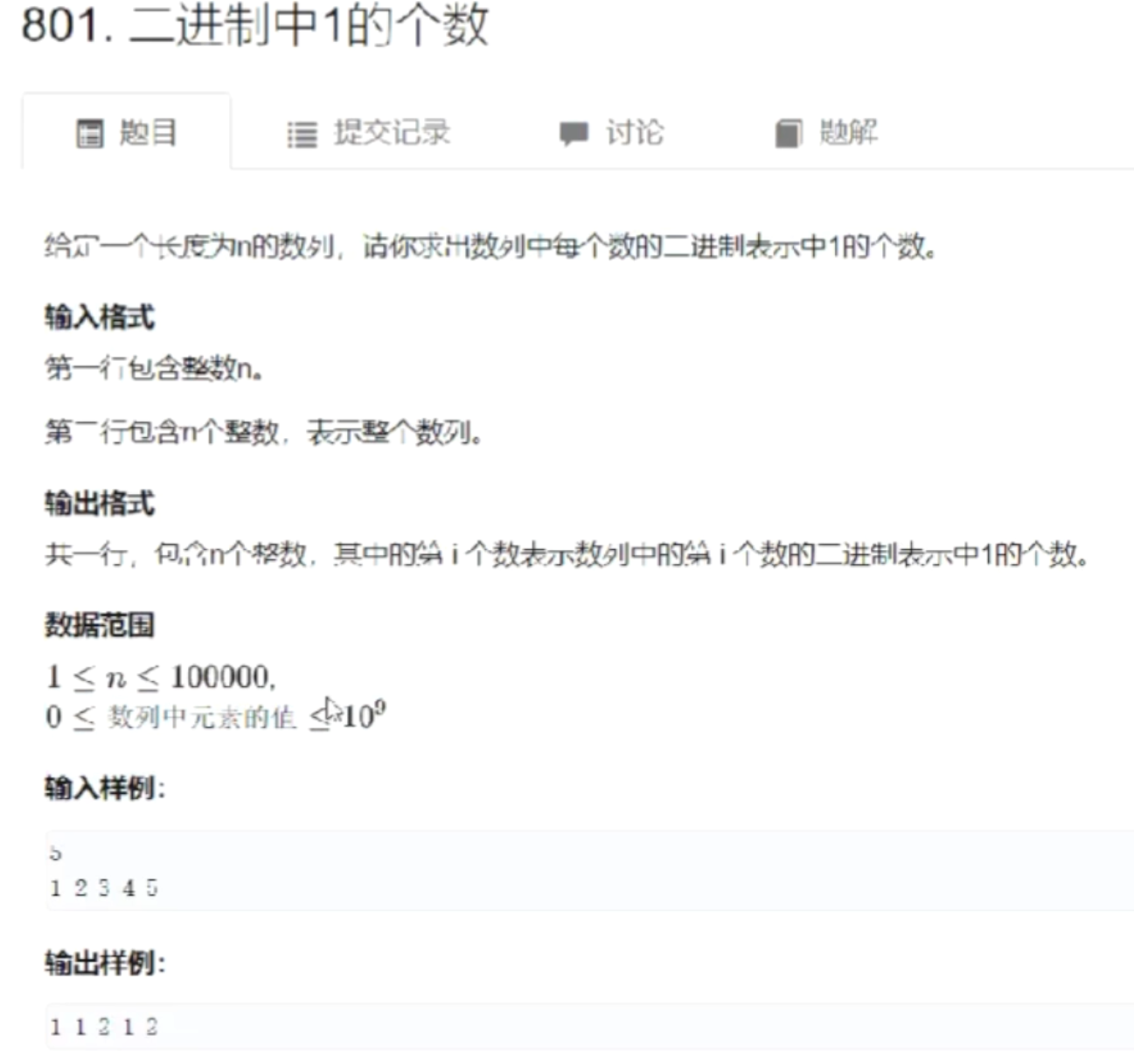
位运算

求n的二进制表示中的第k位数字

算法思想

※求n的二进制表示中的第k位数字：n >> k & 1

①先把第k位移到最后一位：n >> k;

②看个位是几: x & 1

完整代码

//n的二进制表示中的第k位数字
#include<iostream>
using namespace std;

int main(){
    int n = 10;
    for(int k = 3;k >= 0;k --)  cout << (n >> k & 1);
    return 0;
}

返回n的最后一位1

算法思想

※返回n的最后一位1：lowbit(n) -> n & - n

例题

完整代码

//二进制数中1的个数
#include<iostream>
using namespace std;

int lowbit(int x){
    return x & -x;
}

int main(){
    int n;                              //进行n次查询
    cin >> n;
    while(n  --){
        int x;
        cin >> x;                       //要查询的数x
        int res = 0;
        while(x) x -= lowbit(x),res ++ ; //每次减去x的最后一个1
        cout << res << endl;
    }
    return 0;
} 

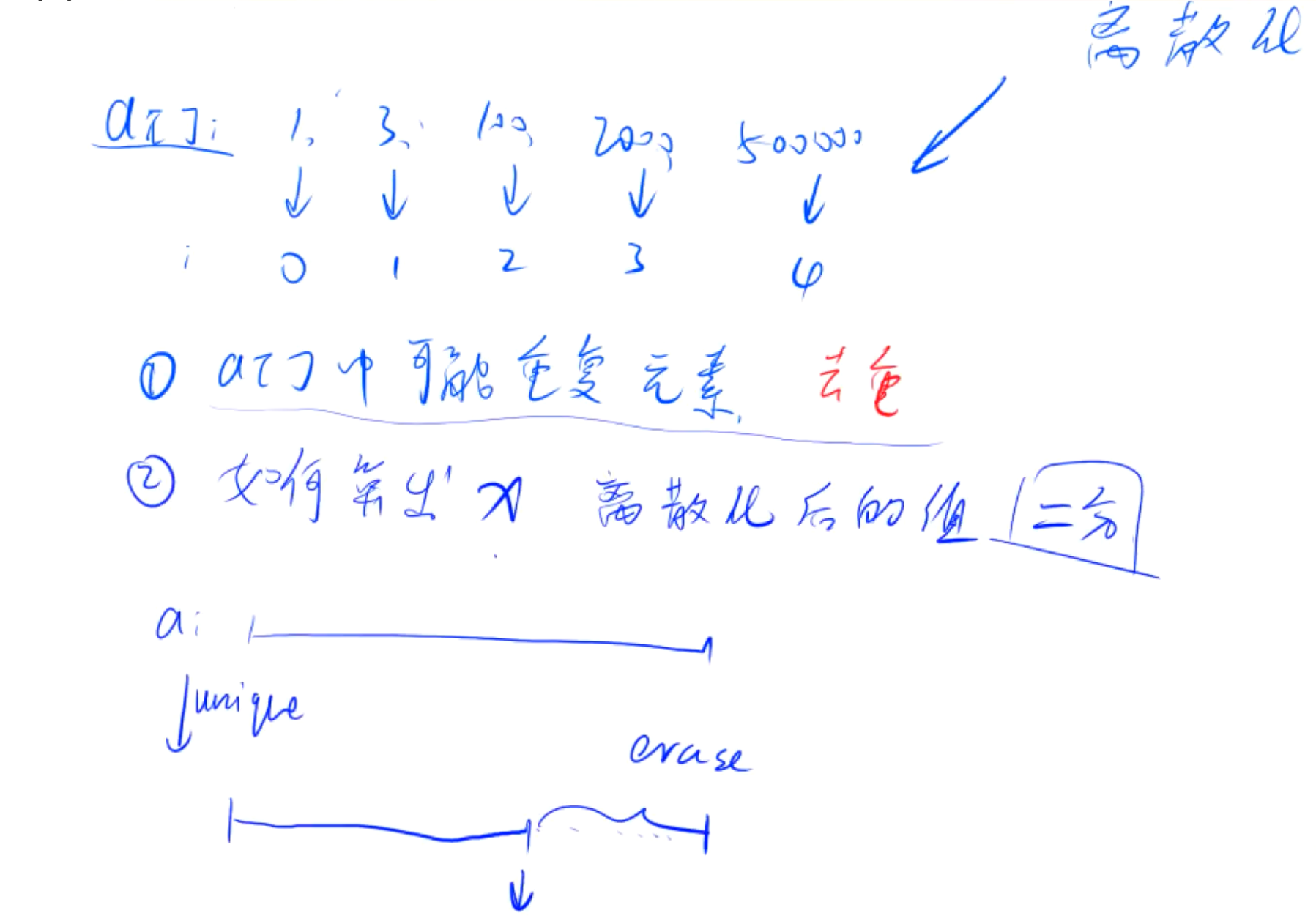
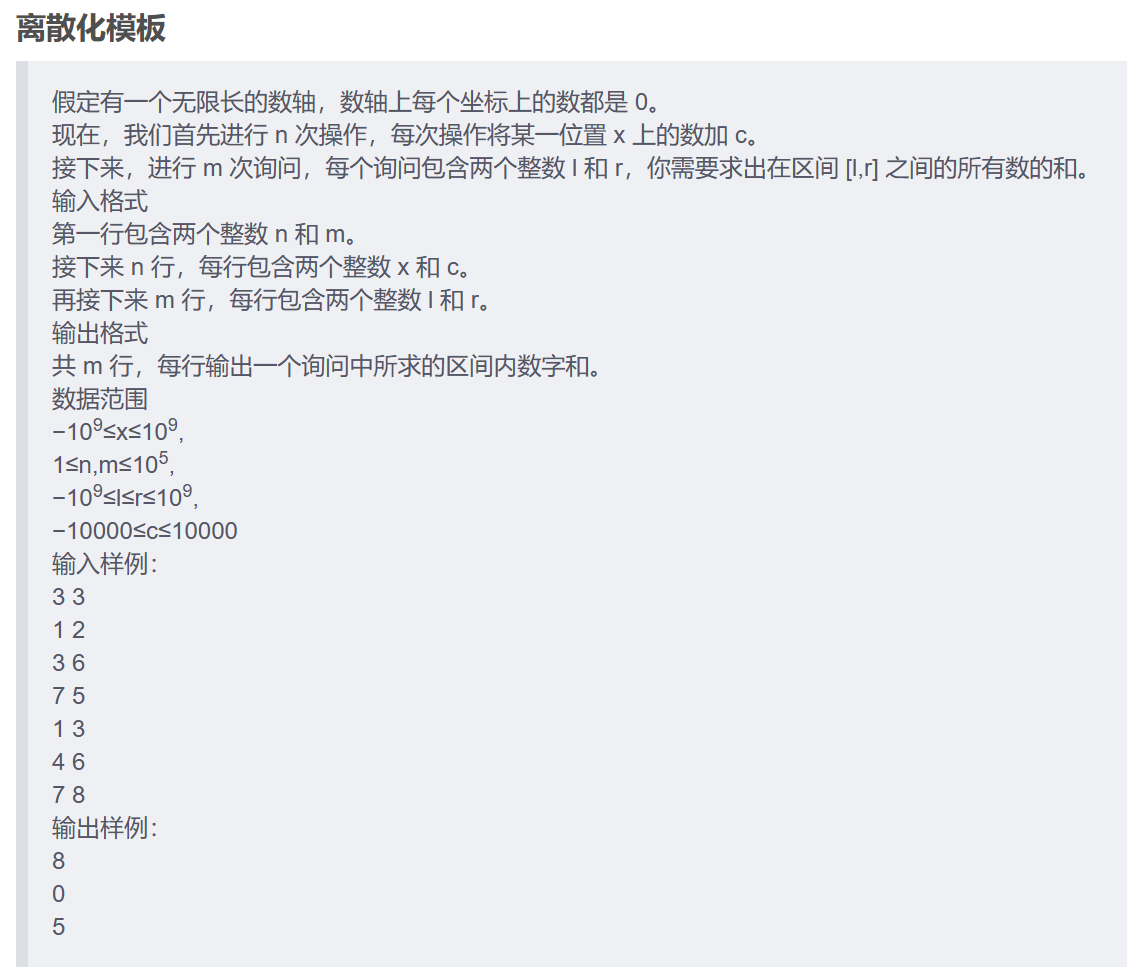
离散化

※加1的话，从1开始映射，不加1的话，从0开始映射

算法思想

1.介绍

离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。离散化本质上可以看成是一种哈希。
2.算法

※unique函数是将数组中所有元素去重，返回去重之后数组的尾端点，使用unique函数必须先排序。
※erase函数是删除unique函数返回的尾端点与数组尾端点的值，也就是删除重复元素

例题

完整代码

//离散化
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 3e6 + 10;
int n ,m;
int a[N],s[N];
typedef pair<int,int> PII;      

vector<int> alls;       //存的所要离散化的元素
vector<PII> add,query; 

int find(int x){
    int l = 0,r = alls.size() - 1;
    while(l < r){
        int mid = l + r >> 1;
        if(alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;
}

int main(){
    cin >> n >> m;
    for(int i = 0;i < n;i ++){
        int x,c;
        cin >> x >> c;
        add.push_back({x, c});
        alls.push_back(x);          //将x加入到待离散化的数组里面去
    }

    for(int i = 0;i < m;i ++){
        int l,r;
        cin >> l >> r;
        query.push_back({l, r});
        alls.push_back(l);          //将左区间加入到待离散化的数组里面去
        alls.push_back(r);          //将右区间加入到待离散化的数组里面去
    }

    //去重
    sort(alls.begin(),alls.end());      //先排序
    alls.erase(unique(alls.begin(),alls.end()),alls.end());     //去掉重复元素
    
    //处理插入
    for(auto item : add){
        int x = find(item.first);   //item.first相当与x
        a[x] += item.second;        //在离散化后的位置加上要加的数  item.second相当于c
    }
   
    //处理前缀和
    for(int i = 1;i <= alls.size();i ++) s[i] = s[i - 1] + a[i];
  
    //处理查询
    for(auto item : query){
        int l = find(item.first), r = find(item.second);
        cout << s[r] - s[l - 1] << endl;
    }
    return 0;
}

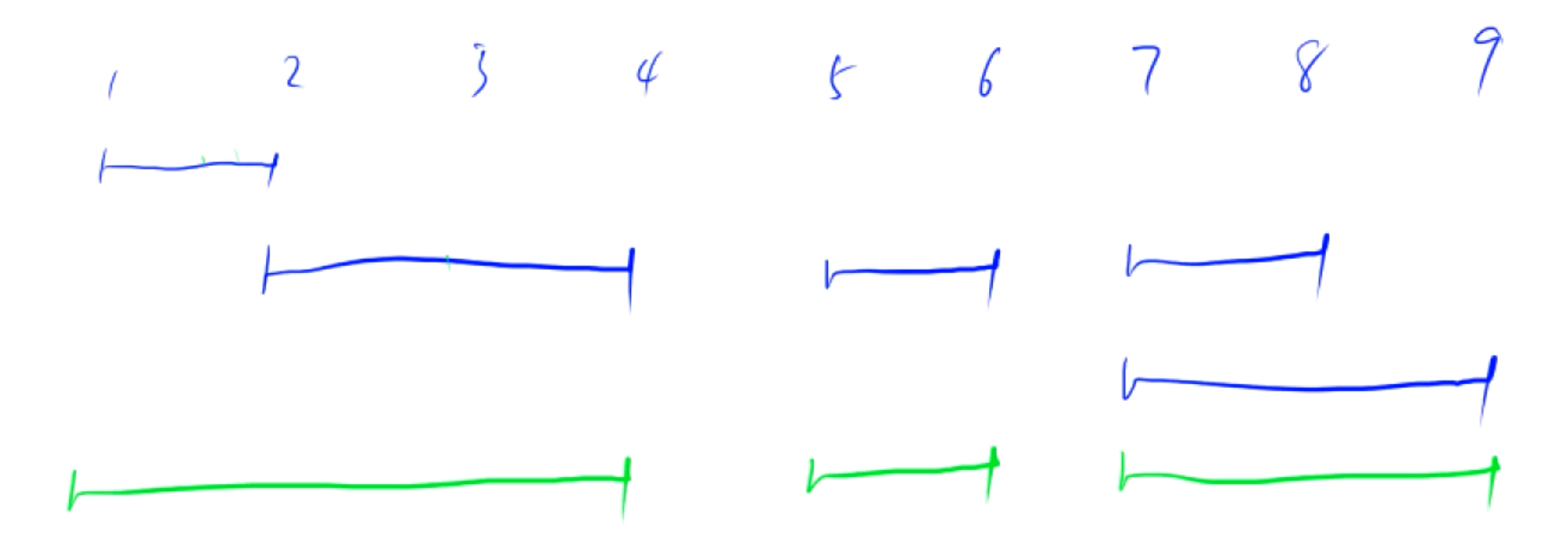
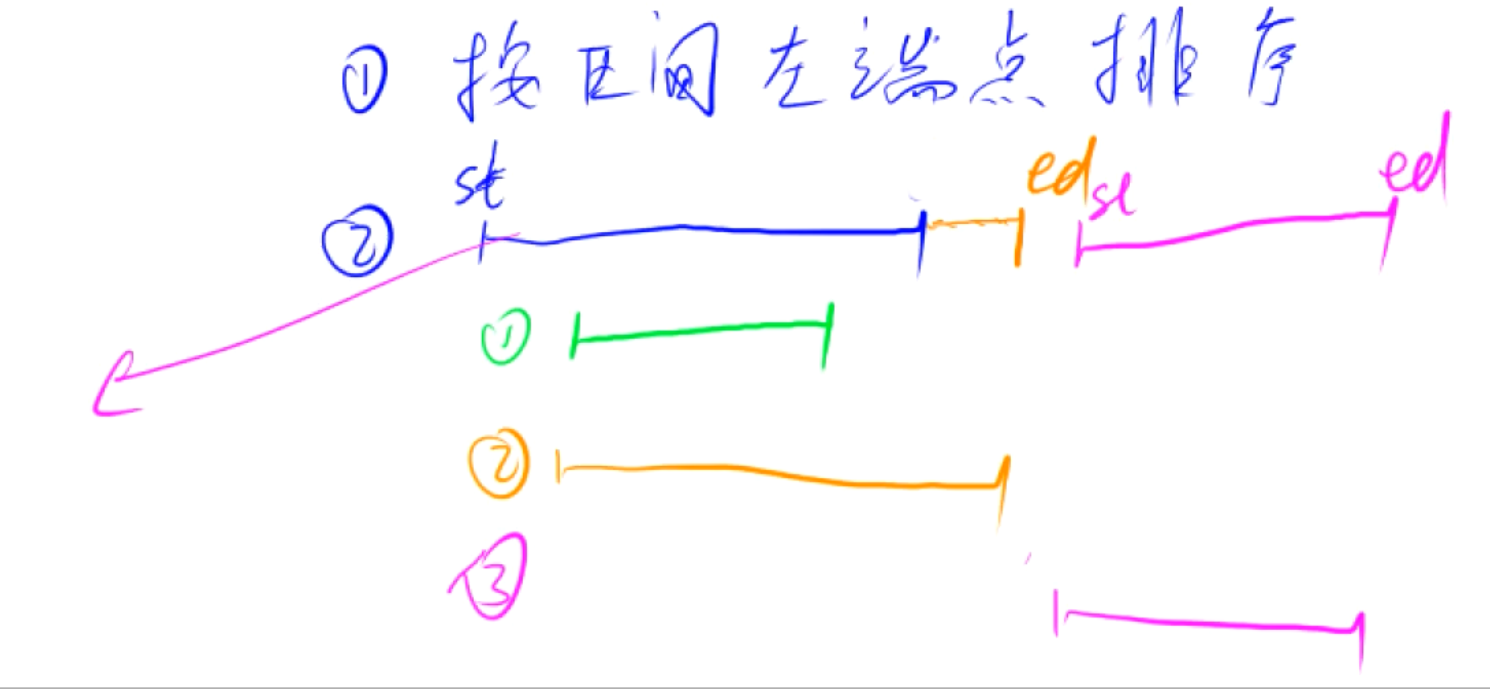
区间合并

算法思想

※图解

1.按区间左端点排序
2.扫描整个区间，扫描过程中，把所有可能有交集的区间进行合并

完整代码

//区间合并
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
typedef pair<int,int> PII;
const int N = 1e6 + 10;
int n ;
vector<PII> segs;

void merge(vector<PII> &segs){
    vector<PII> res;
    sort(segs.begin(),segs.end());      //对pari，优先以左端点排序，再以右端点排序
    int st = -2e9,ed = -2e9;
    for(auto seg:segs){
        if(ed < seg.first){
            if(st != -2e9)
                res.push_back({st,ed});
            st = seg.first,ed = seg.second;
        }
        else{
            ed = max(ed,seg.second);
        }
    }
    if(st != -2e9) res.push_back({st,ed});
    segs = res;
}
int main(){
    cin >> n;
    for(int i = 0;i < n;i ++){
        int l,r;
        cin >> l >> r;
        segs.push_back({l,r});
    }

    merge(segs);
    cout << segs.size() << endl;
    return 0;
}