第一次习题课

第K个数(快速选择)

算法思想

🔺快排思想
※找到分界点x，q[l],q[(l + r) >> 1],q[r].
※左边所有数Left <= x,右边所有数Right >= x.
※递归排序Left，递归排序Right
🔺快选思想
※找到分界点x，q[l],q[(l + r) >> 1],q[r].
※左边所有数Left <= x,右边所有数Right >= x.
※统计x左边所有数的个数S_l,和右边所有数的个数S_r.
※①当K <= S_l时，则递归左边区间 要查找的个数为S_l
※②当K > S_l时，则递归右边区间 要查找的个数应变为K - S_l
※时间复杂度o(n).

完整代码

#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int n,k;
int q[N];

int quick_sort(int l,int r,int k){      //C++中，局部变量与全局变量重名时，优先使用局部变量
    if (l == r)                         //快排里面必须写>=,而快选2个均可
        return q[l];                    //当递归只剩一个数时，则是要查找的数
    int i = l - 1,j = r + 1,x = q[l];
    while(i < j){
        do i ++;while(q[i] < x);
        do j --;while(q[j] > x);
        if(i < j) swap(q[i],q[j]);
    }
    int sl = j - l + 1;     //左半边区间是[l,j]，右半区间是[j+1,r],所以sl = j - l + 1;
    if(k <= sl) return quick_sort(l,j,k);
    return quick_sort(j+1,r,k-sl);      //整个区间第K小个数，相当于是右半区间第K-sl小个数
}

int main(){
    cin >> n >> k ;
    for(int i = 0;i < n;i ++) scanf("%d",&q[i]);
    cout << quick_sort(0,n - 1,k) << endl;
    return 0;
}

逆序对的数量

算法思想

🔺归并排序思想
※[L,R] => 分为[L,mid],[mid + 1,R]
※递归排序[L,mid]和[mid + 1,R]
※归并，将左右两个有序序列合并成一个有序序列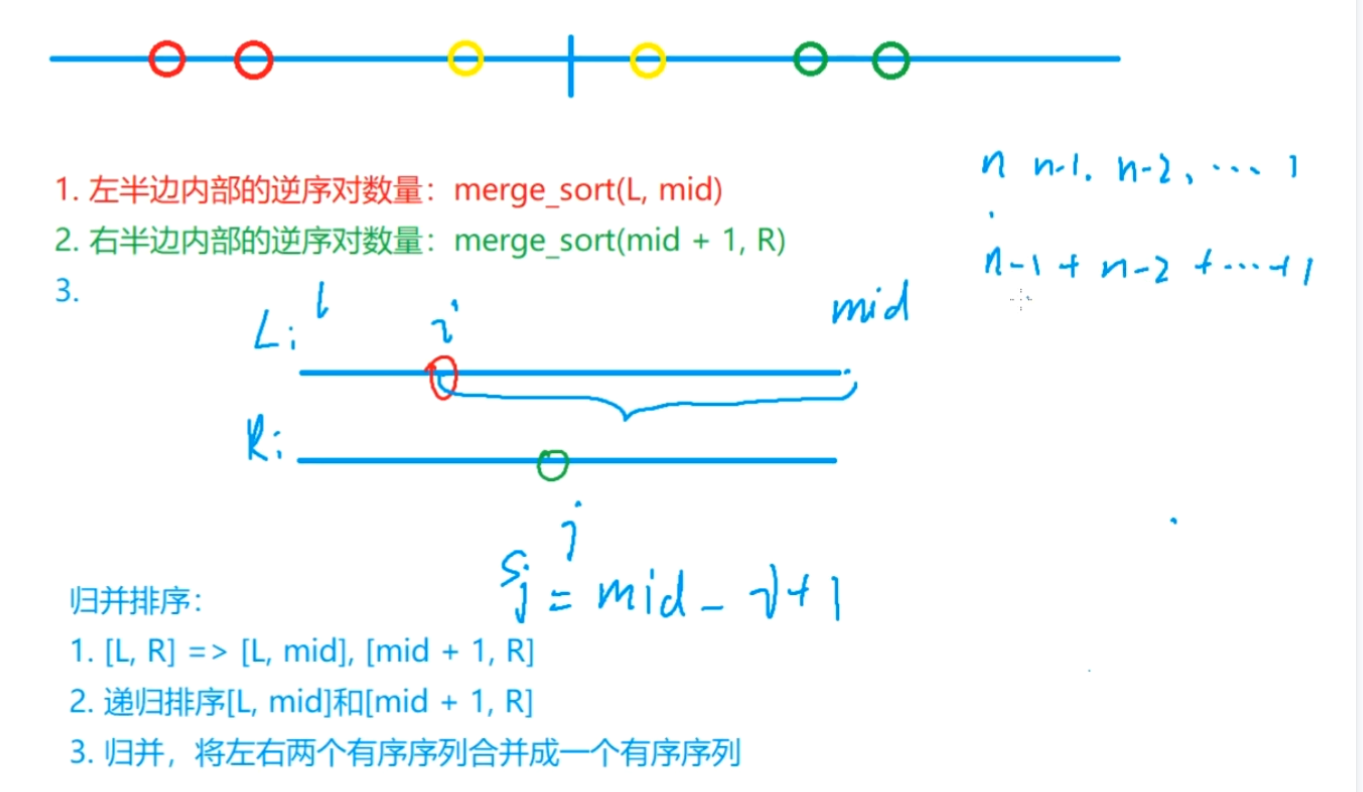

完整代码

//逆序对的数量
#include<iostream>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
int q[N],temp[N];
int n;
LL merge_sort(int l,int r){
    if(l >= r)
        return 0;
    int mid = l + r >> 1;
    LL res = merge_sort(l,mid) + merge_sort(mid + 1,r);
    int k = 0,i = l,j = mid + 1;
    while(i <= mid && j <= r){
        if(q[i] <= q[j])     temp[k ++] = q[i ++];
        else {
            temp[k ++] = q[j ++];
            res += mid - i + 1;
        }
    }
    while(i <= mid) temp[k ++] = q[i ++];
    while(j <= r) temp[k ++] = q[j ++];
    for(int i = l,j = 0;i <= r;i++,j++){
        q[i] = temp [j];
    }
    return res;
}

int main(){
    cin >> n ;
    for(int i = 0;i < n;i ++) scanf("%d",&q[i]);
    cout << merge_sort(0,n - 1) << endl;
    return 0;
}

数的三次方根

算法思想

与浮点二分一样 只是判断条件不同而已。

完整代码

//求数的三次方根
#include<iostream>
using namespace std;

int main(){
    double x;
    cin >> x;
    double l = -10000,r = 10000;
    while(r - l > 1e-8){
        double mid = (l + r) / 2 ;
        if(mid * mid * mid >=x)  r = mid;
        else l = mid;
    }
    printf("%lf\n",l);
    return 0;
}

前缀和

算法思想

与一维前缀和算法一致

完整代码

//前缀和
#include<iostream>
using namespace std;
int n,m;
const int N = 1e6 + 10;
int a[N],S[N];

int main(){
    cin >> n >> m;
    for(int i = 1;i <= n;i ++) cin >> a[i];
    for(int i = 1;i <= n;i ++) S[i] = S[i - 1] + a[i];
    while(m --){
        int l,r;
        cin >> l >> r;
        printf("%d\n",S[r]-S[l - 1]);
    }
    return 0;
}

子矩阵的和

算法思想

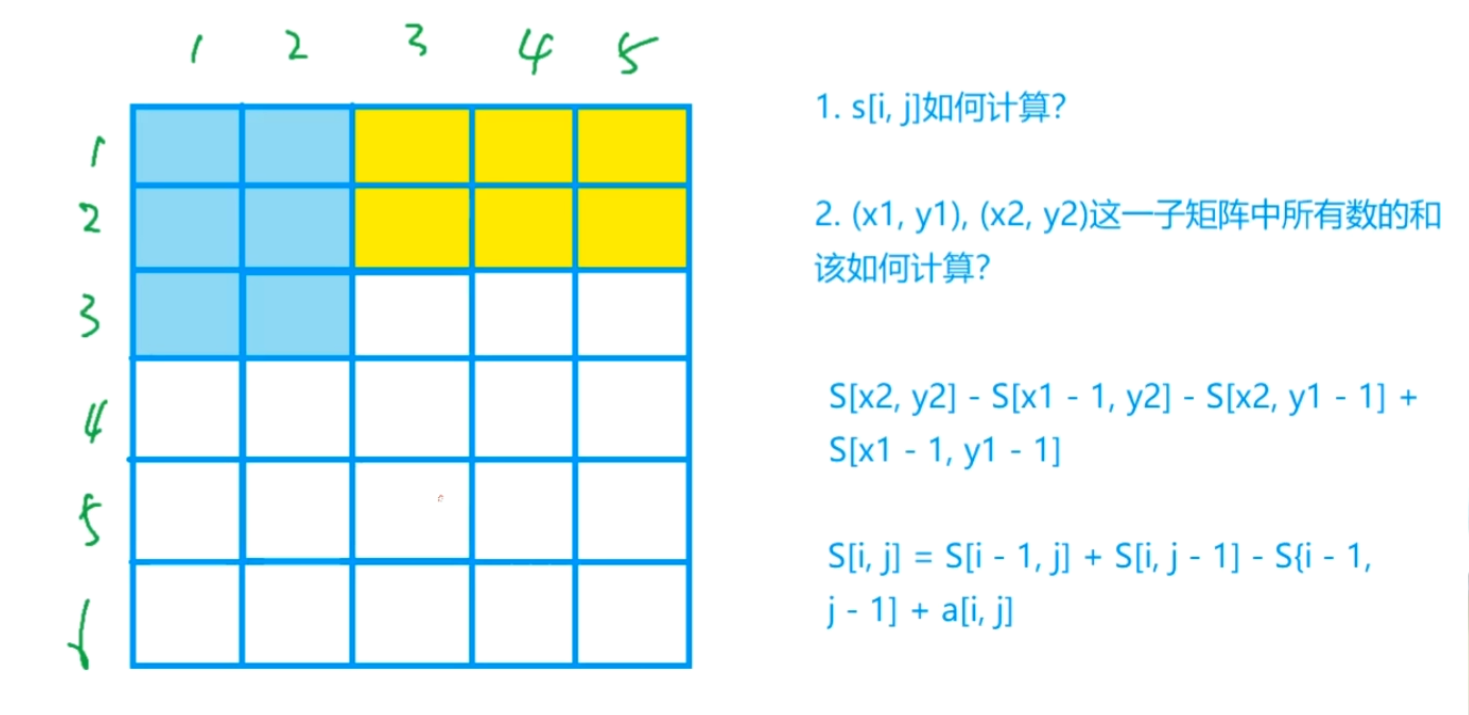
完整代码

//子矩阵的和
#include<iostream>
using namespace std;
const int N = 1010;
int n,m,q;
int a[N][N],s[N][N];

int main(){
    scanf("%d%d%d",&n,&m,&q);
    for(int i = 1;i <= n;i ++)
        for(int j = 1;j <= m;j ++)
            scanf("%d",&a[i][j]);
    for(int i = 1;i <= n;i ++)
        for(int j = 1;j <= m ;j ++)
            s[i][j] = s[i - 1][j] + s[i][j - 1] -s[i -1][j - 1] + a[i][j];
    while(q--){
        int x1,x2,y1,y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%d\n",s[x2][y2]-s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }
    return 0;
}

一维差分

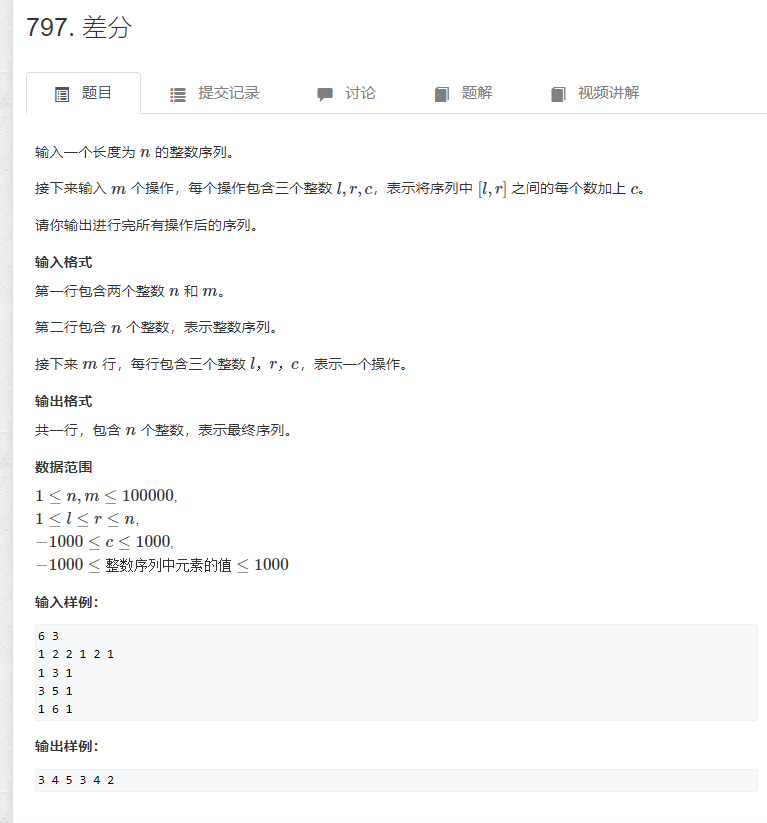
算法思想

完整代码

// 一维差分
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int n,m;
int a[N],b[N];

void insert(int l,int r,int c){
    b[l] += c;
    b[r + 1] -= c;
}

int main(){
    cin >> n >> m;
    for(int i = 1;i <= n;i ++) cin >> a[i];
    for(int i = 1;i <= n;i ++) insert(i,i,a[i]);
    while(m --){
        int l,r,c;
        cin >> l >> r >> c;
        insert(l,r,c);
    }
    for(int i = 1;i <= n;i ++) a[i] = a[i - 1] + b[i];
    for(int i = 1;i <= n; i ++) printf("%d ",a[i]);
    puts(" ");
    return 0;
}

差分矩阵

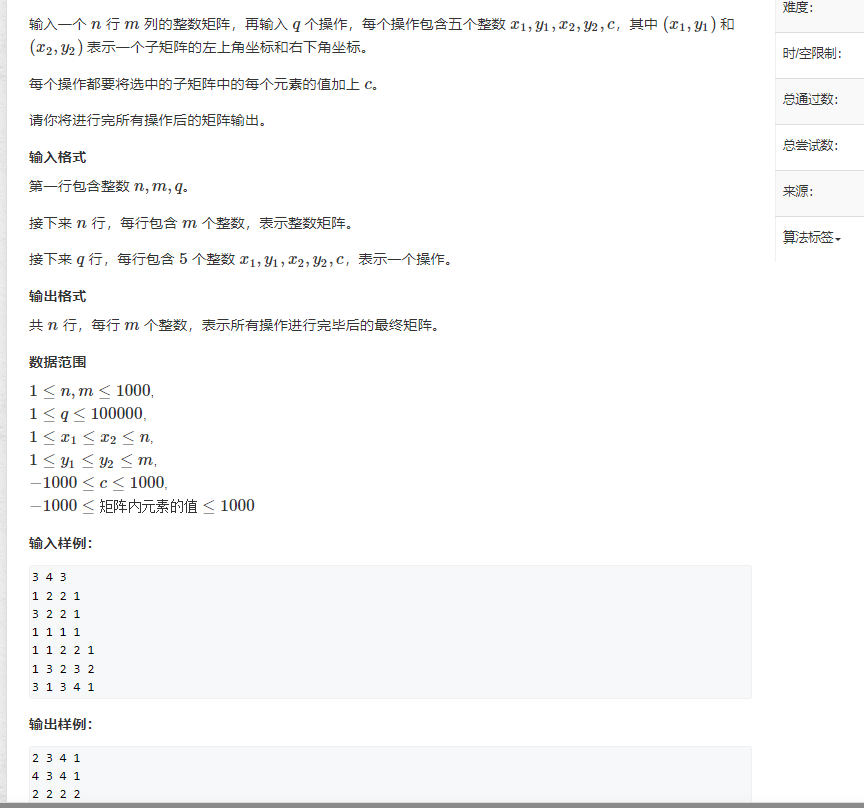
算法思想

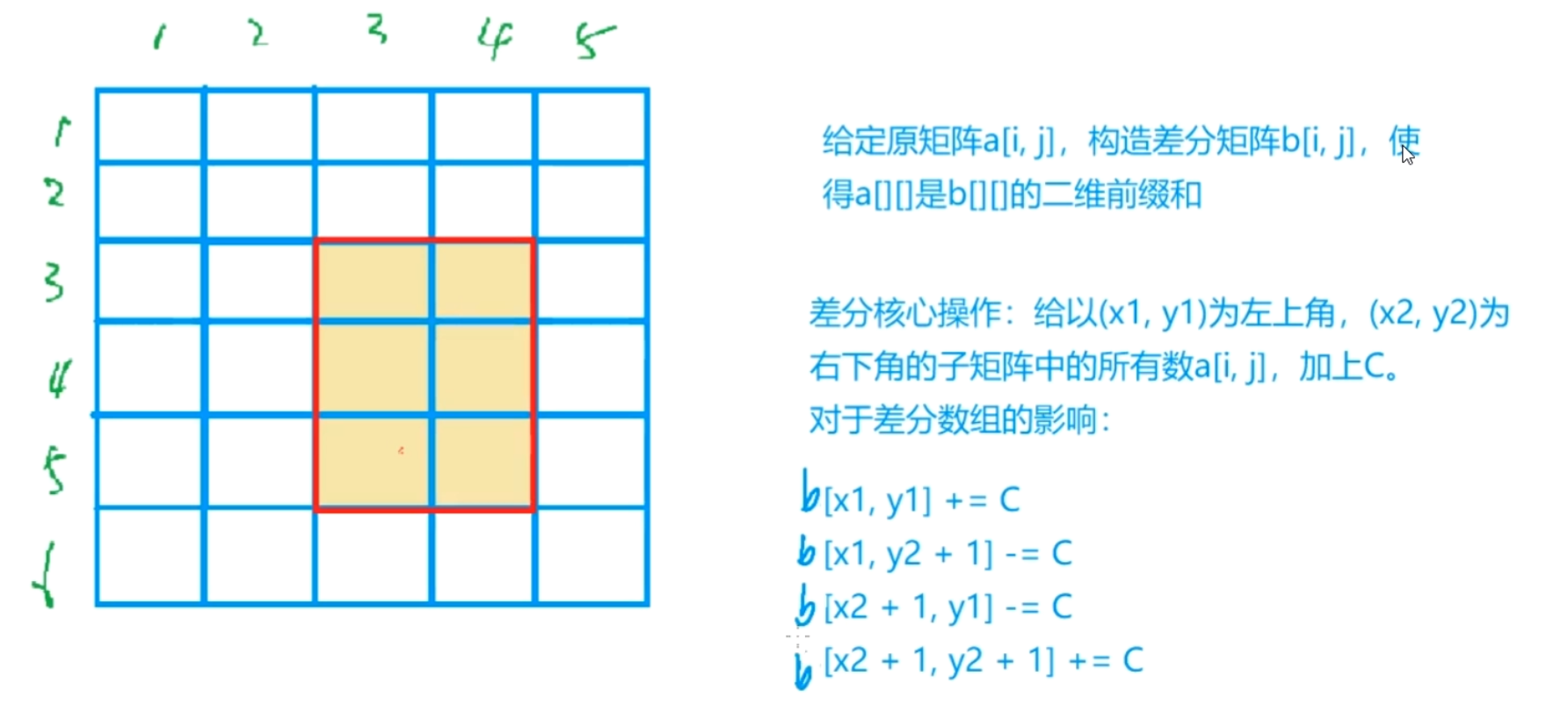
完整代码

#include<iostream>
using namespace std;
const int N = 1010;
int n,m,q;
int a[N][N],b[N][N];

void insert(int x1,int y1,int x2,int y2,int c){
    b[x1][y1] += c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main(){
    scanf("%d%d%d",&n,&m,&q);
    for(int i = 1;i <= n;i ++){
        for(int j = 1;j <= m;j ++){
            scanf("%d",&a[i][j]);
            insert(i,j,i,j,a[i][j]);
        }
    }
    while(q--){
        int x1,y1,x2,y2,c;
        scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
        insert(x1,y1,x2,y2,c);
    }
    for(int i = 1;i <= n;i ++){
        for(int j = 1;j <= m;j ++){
            a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];
        }
    }
    for(int i = 1;i <= n;i ++){
        for(int j = 1;j <= m;j ++){
            printf("%d ",a[i][j]);
        }
        printf("\n");
    }
    return 0;
}