排序
快速排序
算法思想
分治
1.确定分界点—-mid = (l + r) / 2
2.递归排序left、right
3.归并–合二为一
完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| #include<iostream>
using namespace std;
const int N = 1e6 +10;
int q[N];
int temp[N];
int n;
void merge_sort(int q[],int l,int r){
if(l>=r)
return;
int mid = l + r >> 1;
merge_sort(q,l,mid),merge_sort(q,mid+1,r);
int k = 0,i = l,j = mid +1;
while(i <= mid && j <= r)
if(q[i] <= q[j]) temp[k++] = q[i++];
else temp[k++] = q[j++];
while(i <= mid) temp[k++] = q[i++];
while(j <= r) temp[k++] = q[j++];
for(i = l,j = 0;i <= r;i++,j++)
q[i] = temp[j];
}
int main(){
scanf("%d",&n);
for(int i = 0;i < n;i ++){
scanf("%d",&q[i]);
}
merge_sort(q,0,n-1);
for(int i = 0;i < n;i++){
printf("%d\t",q[i]);
}
return 0;
}
|
代码模板:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void merge_sort(int q[],int l,int r){
if(l >= r)
return;
int mid = l + r >> 1;
merge_sort(q,l,mid),merge_sort(q,mid+1,r);
int k = 0,i = l,j = mid + 1;
while(i <= mid && j<= r)
if(q[i] < q[j]) temp[k++] = q[i];
else temp[k++] = q[j];
while(i <= mid) temp[k++] = q[i++];
while(j <= r) temp[k++] = q[j++];
for(i = l, j = 0;i <= r;i++,j++)
q[i] = temp[j];
}
|
算法图解
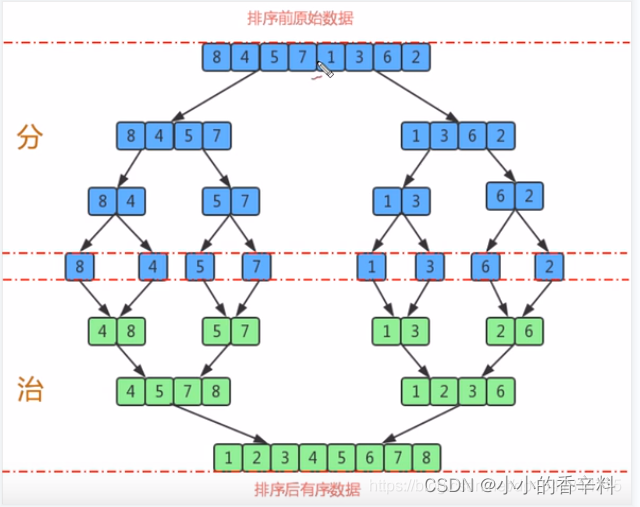
归并排序算法的特点
1.时间复杂度
归并排序算法每次将序列折半分组,共需要logn轮,因此归并排序算法的时间复杂度是O(nlogn)
2.空间复杂度 \
归并排序算法排序过程中需要额外的一个序列去存储排序后的结果,所占空间是n,因此空间复杂度为O(n)
3.稳定性
归并排序算法排序过程中需要额外的一个序列去存储排序后的结果,所占空间是n,因此空间复杂度为O(n)
